Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T13:02:22.168Z Has data issue: false hasContentIssue false
  • English
  • Français

Primes in Short Segments of Arithmetic Progressions

Published online by Cambridge University Press:  20 November 2018

D. A. Goldston  and
C. Y. Yildirim
D. A. Goldston
Affiliation:
Department of Mathematics and Computer Science San Jose State University San Jose, California 95192 U.S.A., e-mail: yalcin@sci.bilkent.edu.tr
C. Y. Yildirim
Affiliation:
Department of Mathematics Bilkent University Ankara 06533 Turkey, e-mail: goldston@mathcs.sjsu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the variance for the number of primes that are both in the interval 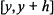$\left[ y,\,y\,+\,h \right]$ for 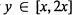$y\,\in \,[x,\,2x]$ and in an arithmetic progression of modulus $q$. We study the total variance obtained by adding these variances over all the reduced residue classes modulo $q$. Assuming a strong form of the twin prime conjecture and the Riemann Hypothesis one can obtain an asymptotic formula for the total variance in the range when 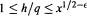$1\le \,h/q\,\le \,{{x}^{1/2-\in }}$, for any 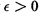$\varepsilon \,>\,0$. We show that one can still obtain some weaker asymptotic results assuming the Generalized Riemann Hypothesis (GRH) in place of the twin prime conjecture. In their simplest form, our results are that on GRH the same asymptotic formula obtained with the twin prime conjecture is true for “almost all” $q$ in the range 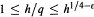$1\le h/q\le {{h}^{1/4-\in }}$, that on averaging over $q$ one obtains an asymptotic formula in the extended range 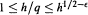$1\le h/q\le {{h}^{1/2-\in }}$, and that there are lower bounds with the correct order of magnitude for all $q$ in the range 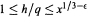$1\le h/q\le {{x}^{1/3-\in }}$.

Keywords

11M26
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 3 , 01 June 1998 , pp. 563 - 580
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Davenport, H., Multiplicative Number Theory, second edition, revised by Montgomery, H.L., Springer- Verlag, Berlin, 1980.Google Scholar
2. Friedlander, J.B. and Goldston, D.A., Variance of distribution of primes in residue classes. Quart. J. Math. Oxford Ser. (2) 47(1996), 313-336.Google Scholar
3. Friedlander, J.B. and Goldston, D.A., Note on a Variance in the Distribution of Primes. Proceedings of the Schinzel Conference, July 1997, Zakopane, Poland, de Gruyter.Google Scholar
4. Goldston, D.A., A lower bound for the second moment of primes in short intervals. Exposition Math. 13(1995), 366-376.Google Scholar
5. Goldston, D.A. and Montgomery, H.L., Pair correlation of zeros and primes in short intervals. In: Analytic Number Theory and Diophantine Problems, Birkhaüser, Boston, Massachusetts, 1987, 183—203.Google Scholar
6. Hooley, C., On the Barban-Davenport-Halberstam theorem: VI. J. London Math. Soc. (2) 13(1976), 57-64.Google Scholar
7. Kaezorowski, J., Perelli, A. and Pintz, J., A note on the exceptional set for Goldbach's problem in short intervals. Monatsh. Math. 116(1993), 275-282.Google Scholar
8. Languasco, A. and Perelli, A., A pair correlation hypothesis and the exceptional set in Goldbach 's problem. Mathematika 43(1995), 349-361.Google Scholar
9. Montgomery, H.L., Multiplicative Number Theory. Lecture Notes in Math. 227, Springer-Verlag, Berlin, 1971.Google Scholar
10. Özlük, A. E., On the q-analogue of the pair correlation conjecture. J. Number Theory 59(1996), 319-351.Google Scholar
11. Prachar, K., Generalisation of a theorem of A. Selberg on primes in short intervals. In: Topics in Number Theory, Colloquia Mathematica Societatis Janos Bolyai 13, Debrecen, 1974, 267-280.Google Scholar
12. Yildiran, C.Y., The pair correlation of zeros of DirichletL-functions and primes in arithmetic progressions. ManuscriptaMath. 72(1991), 325-334.Google Scholar