Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-15T01:47:18.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Products of Reflections in an Affine Moufang Plane

Published online by Cambridge University Press:  20 November 2018

K. Martin Götzky
K. Martin Götzky*
Affiliation:
University of Toronto, Toronto, Ontario University of Kiel, Kiel, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 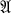be a Moufang plane. By specializing one line ω, the line at infinity, weobtain an affine Moufang plane 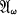. The group generated by the shears of 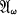is called the equiaffine group. Veblen [9, § 52] asked whether every equiaffinity is a product of two affine reflections. He gave a proof which will work in an affine Pappian plane, using the following two properties.

Property 1. If an equiaffinity fixes two distinct proper points of 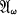, it fixes every point collinear with them.

Property 2. Let e be an equiaffinity and P a point such that ppe2pe3 is a triangle. Then the lines PePe2 and PPe3 are parallel.

Without using these properties, it will be proved that the answer to Veblen's question is “yes“ if and only if the Moufang plane 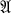is Pappian.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 3 , 01 June 1970 , pp. 666 - 673
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Artin, E., Geometric algebra, Interscience Tracts, No. 3 (Interscience, New York, 1957).Google Scholar
2. Bachmann, F., Aufbau der Géométrie aus dem Spiegelungsbegriff (Die Grundlehren der mathematischen Wissenschaften, Band XCVI (Springer-Verlag, Berlin-Göttingen-Heidelberg, 1959).Google Scholar
3. Coxeter, H. S. M., A finely regular polygons, Abh. Math. Sem. Univ. Hamburg 34 (1969), 38–58.Google Scholar
4. Coxeter, H. S. M., Products of shears in an affine Pappian plane, Rend. Mat. Pura Appl. (1970).Google Scholar
5. Giinter, Ewald, Eine Gruppentheoretische BegrÜndung der ebenen affinen Géométrie, Arch. Math. 18 (1967), 100–106.Google Scholar
6. Rolf, Lingenberg, Über Gruppen, projektiver Kollineationen, welche eine perspective Dualitdt invariant lassen, Arch. Math. 13 (1962), 385–400.Google Scholar
7. Martin, Götzky, Eine Kennzeichnung der orthogonalen Gruppen unter den unitdren Gruppen, Arch. Math. 15 (1964), 261–265.Google Scholar
8. Giinter, Pickert, Projektive Ebenen, Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berucksichtigung der Anwendungsgebiete, Band LXXX (Springer-Verlag, Berlin-Göttingen-Heidelberg, 1955).Google Scholar
9. Veblen, O. and Young, J. W., Projective geometry, Vol. II (Ginn and Company, Boston, 1918).Google Scholar