Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-14T23:10:01.443Z Has data issue: false hasContentIssue false
  • English
  • Français

Produit Tensoriel Topologique de Corps Values

Published online by Cambridge University Press:  20 November 2018

Jean Fresnel  and
Michel Matignon
Jean Fresnel
Affiliation:
U.E.R. de Mathématiques et d'Informatique, Laboratoire associé au CNRS n° 226, Talence, France
Michel Matignon
Affiliation:
U.E.R. de Mathématiques et d'Informatique, Laboratoire associé au CNRS n° 226, Talence, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soient K un corps local, 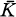sa clôture algébrique, R, L, M trois corps tels K ⊂ R ⊂ L ⊂ 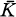et K ⊂ R ⊂ M ⊂ 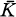. Supposons que L et M soient linéairement disjoints sur R. Quel est le complété du corps LM (compositum de L et M) pour une norme de R-algèbre qui coïncide avec la valeur absolue sur L ∪ M? On sait que LM est isomorphe en tant que R-algèbre au produit tensoriel L ⨂RM et il est facile de montrer que la valeur absolue est la plus petite norme du type considéré ci-dessus et que la norme tensorielle en est la plus grande. C'est pourquoi nous étudions d'abord le complété de L ⊗RM pour la norme tensorielle. Citons dans ce cas les résultats essentiels lorsque la caractéristique de K est nulle.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 2 , 01 April 1983 , pp. 218 - 273
Copyright
Copyright © Canadian Mathematical Society 1983

References

Bibliographie

1. Ax, J., Zeros of polynomials over local fields. The Galois action, Journal of Algebra 15 (1970), 417–428.Google Scholar
2. Bourbaki, N., Topologie générale, ch. 3 (Hermann, Paris, 1971).Google Scholar
3. Bourbaki, N., Algèbre, ch. 3 (Hermann, Paris, 1970).Google Scholar
4. Bourbaki, N., Algèbre, ch. 5, 2e edition (Hermann, Paris, 1959).Google Scholar
5. Bourbaki, N., Algèbre, ch. 8 (Hermann, Paris, 1958).Google Scholar
6. Bourbaki, N., Théories spectrales, ch. 1 (Hermann, Paris, 1967).Google Scholar
7. Fresnel, J. et de Mathan, B., Algèbres L1 p-adiques, Bull. Soc. Math. France 106 (1978), 225–260.Google Scholar
8. Fresnel, J. et de Mathan, B., Algèbre d'un monoïde, idéaux de L ⊗ R M et idéaux fermés de (non publié).Google Scholar
9. Gruson, L., Théorie de Fredholm p-adique, Bull. Soc. Math. France 94 (1966), 67–95.Google Scholar
10. Matignon, M., Sous-corps fermés du complété de la clôture algébrique d'un corps local, C.R.A.S. Acad. Se. Paris 288 (1979), 1051–1054.Google Scholar
11. Matignon, M., Sous-corps fermés du complété de la clôture algébrique d'un corps local, Thèse de 3e cycle, Bordeaux (1979).Google Scholar
12. Monna, A. F., Analyse non archimédienne, Erg. der. Math. (Springer Verlag, 1970).Google Scholar
13. Parmenter, M. M. and Sehgal, S. K., Non archimedean group algebras, Journal of Number Theory 7 (1975), 376–384.Google Scholar
14. van Rooij, A. C. M., Non archimedean functional analysis (Pure and applied mathematics, New York, Dekker, 1977).Google Scholar
15. van Rooij, A. C. M. and Schikhof, W. H., Non archimedean commutative C*-algebras, Proceedings of the koninklijke nederlandse akademie van wetenshappen 76 (1973), 381–389.Google Scholar
16. Sen, S., On automorphisms of local fields, Annals of Math. 90 (1969), 33–40.Google Scholar
17. Serre, J.-P., Corps locaux (Hermann, 2e édition, 1968).Google Scholar
18. Serre, J.-P., Endomorphismes complètement continus des espaces de Banach p-adique, I.H.E.S., Publications Mathématiques, n° 12.Google Scholar
19. Tate, J., p-divisible groups, Proceedings on a conference on local fields.Google Scholar