Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Burbea, Jacob
1982.
The Cauchy and the Szegö kernels on multiply connected regions.
Rendiconti del Circolo Matematico di Palermo,
Vol. 31,
Issue. 1,
p.
105.

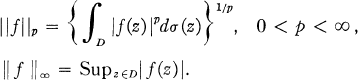
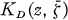 be the Bergman kernel of
be the Bergman kernel of