Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-29T09:50:37.449Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadratic forms over Quadratic Extensions of Fields with Two Quaternion Algebras

Published online by Cambridge University Press:  20 November 2018

Craig M. Cordes  and
John R. Ramsey Jr.
Craig M. Cordes
Affiliation:
Louisiana State University, Baton Rouge, Louisiana
John R. Ramsey Jr.
Affiliation:
Louisiana State University, Baton Rouge, Louisiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we analyze what happens with respect to quadratic forms when a square root is adjoined to a field F which has exactly two quaternion algebras. There are many such fields—the real numbers and finite extensions of the p-adic numbers being two familiar examples. For general quadratic extensions, there are many unanswered questions concerning the quadratic form structure, but for these special fields we can clear up most of them.

It is assumed char F ≠ 2 and K = F (√a) where a ∊ Ḟ – Ḟ2. Ḟ denotes the non-zero elements of F. Generally the letters a, b, c, … and α, β, … refer to elements from Ḟ and x, y, z, … come from .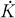

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 5 , 01 October 1979 , pp. 1047 - 1058
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Cordes, C., Kaplansky s radical and quadratic forms over non-real fields, Acta. Arith. 28 (1975), 253–261.Google Scholar
2. Cordes, C., Quadratic forms over non-formally real fields with a finite number of quaternion algebras, Pac. J. of Math. 63 (1976), 357–365.Google Scholar
3. Cordes, C. and Ramsey, J., Quadratic forms over fields with u = q/2 < ∞, Fund. Math. 99 (1978), 1–10.Google Scholar
4. Elman, R. and Lam, T. Y., Quadratic forms under algebraic extensions, Math. Ann. 219 (1976), 21–42.Google Scholar
5. Gross, H. and Fischer, H. R., Non-real fields k and infinite dimensional k-vector spaces, Math. Ann. 150 (1965), 285–308.Google Scholar
6. Kaplansky, I., Frohlich's local quadratic forms, J. Reine Angew, Math. 239 (1969), 74–77.Google Scholar
7. Lam, T. Y., The algebraic theory of quadratic forms (W. A. Benjamin, Reading, Massachusetts, 1973).Google Scholar
8. Pfister, A., Multaplikative quadratische Formen, Arch. Math. 16 (1965), 363–370.Google Scholar
9. Scharlau, W., Quadratic forms, Queen's papers on pure and applied mathematics No. 22 (Kingston, Ontario, 1969).Google Scholar
10. Szczepanik, L., Quaternion algebras and binary quadratic forms, Univ. Slaski W. Katowicach Prace Naukowe No. 87 Prace Mat. No. 6 (1975), 17–27.Google Scholar
11. Szymiczek, K., Quadratic forms over fields with finite square class number, Acta. Arith. 28 (1975), 195–221.Google Scholar