Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T22:55:07.370Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadratic Integers and Coxeter Groups

Published online by Cambridge University Press:  20 November 2018

Norman W. Johnson  and
Asia Ivić Weiss
Norman W. Johnson
Affiliation:
Department of Mathematics and Computer Science, Wheaton College, Norton, Massachusetts 02766, USA
Asia Ivić Weiss
Affiliation:
Department of Mathematics and Statistics, York University, Toronto, Ontario, M3J 1P3
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Matrices whose entries belong to certain rings of algebraic integers can be associated with discrete groups of transformations of inversive 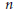$n$-space or hyperbolic 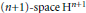$(n+1)-\text{space}\,{{\text{H}}^{n+1}}$. For small 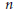$n$, these may be Coxeter groups, generated by reflections, or certain subgroups whose generators include direct isometries of 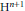${{\text{H}}^{n+1}}$. We show how linear fractional transformations over rings of rational and (real or imaginary) quadratic integers are related to the symmetry groups of regular tilings of the hyperbolic plane or 3-space. New light is shed on the properties of the rational modular group 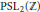$\text{PS}{{\text{L}}_{2}}(\mathbb{Z})$, the Gaussian modular (Picard) group 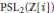$\text{PS}{{\text{L}}_{2}}(\mathbb{Z}[i])$, and the Eisenstein modular group 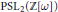$\text{PS}{{\text{L}}_{2}}(\mathbb{Z}\left[ \omega \right])$.

Keywords

11F0620F5520G2020H1022E40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 6 , 01 December 1999 , pp. 1307 - 1336
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Alperin, R. C., Normal subgroups of PSL2(Z[-3]). Proc. Amer.Math. Soc. 124(1996), 2935–2941.Google Scholar
[2] Bianchi, L., Geometrische Darstellung der Gruppen linearer Substitutionenmit ganzen complexen Coefficienten nebst Anwendungen auf die Zahlentheorie. Math. Ann. 38(1891), 313–333; reprinted in Opere vol. I, pt. 1 (Edizione Cremonese, Rome, 1952), 233–258.Google Scholar
[3] Bianchi, L., Sui gruppi de sostituzioni lineari con coeficienti appartenenti a corpi quadratici imaginari. Math. Ann. 40(1892), 332–412; reprinted in Opere vol. I, pt. 1 (Edizione Cremonese, Rome, 1952), 270–373.Google Scholar
[4] Coxeter, H. S. M., Discrete groups generated by reflections. Annals of Math. (2) 35(1934), 588–621; reprinted in Kaleidoscopes: Selected Writings of Coxeter, H. S. M. (eds. Sherk, F. A., P. McMullen, Thompson, A. C., Weiss, A. I.), Wiley, New York, 1995, 145–178.Google Scholar
[5] Coxeter, H. S. M., Regular honeycombs in hyperbolic space. Proc. Internat. Congress of Mathematicians (Amsterdam, 1954), Vol. III, Noordh off, Groningen, and North-Holland, Amsterdam, 1956, 155–169; reprinted in Twelve Geometric Essays, Southern Illinois Univ. Press, Carbondale, IL, and Feffer & Simons, London-Amsterdam, 1968, 199–214.Google Scholar
[6] Coxeter, H. S. M. and Moser, W. O. J., Generators and Relations for Discrete Groups. Ergeb. Math. Grenzgeb. (N. F.), Bd. 14, Springer-Verlag, Berlin-Göttingen-Heidelberg, 1957; 4th edn, idem, Berlin-Heidelberg-New York, 1980.Google Scholar
[7] Coxeter, H. S. M. and Whitrow, G. J., World-structure and non-Euclidean honeycombs. Proc. Roy. Soc. London Ser. A 201(1950), 417–437.Google Scholar
[8] Fine, B., Algebraic Theory of the Bianchi Groups. Pure Appl. Math. 129, Marcel Dekker, New York-Basel, 1989.Google Scholar
[9] Fine, B. and Newman, M., The normal subgroup structure of the Picard group. Trans. Amer. Math. Soc. 302(1987), 769–786.Google Scholar
[10] Fricke, R. and Klein, F., Vorlesungen über die Theorie der automorphen Funktionen. Bd. I, Teubner, Leipzig, 1897; 2nd edn, idem, 1926.Google Scholar
[11] Higman, G., Neumann, B. H. and Neumann, H., Embedding theorems for groups. J. London Math. Soc. 24(1949), 247–254.Google Scholar
[12] Hua, L. K., Introduction to Number Theory. Springer-Verlag, Berlin-Heidelberg-New York, 1982 (translated by P. Shiu from the 1957 Chinese original).Google Scholar
[13] Humphreys, J. E., Reflection Groups and Coxeter Groups. Cambridge University Press, Cambridge-New York, 1990, 1992.Google Scholar
[14] Johnson, N. W., Absolute polarities and central inversions. In: The Geometric Vein: The Coxeter Festchrift (eds. Davis, C., Grunbaum, B. and Sherk, F. A.), Springer-Verlag, New York-Heidelberg-Berlin, 1981, 443–464.Google Scholar
[15] Johnson, N. W. and Weiss, A. I., Quaternionic modular groups. Linear Algebra Appl. 295(1999), 159–189.Google Scholar
[16] Klein, F., Ueber die Transformation der elliptischen Functionen und die Auflösung der Gleichungen fünften Grades. Math. Ann. 14(1879), 111–172; reprinted in Gesammelte mathematische Abhandlungen, Bd. III, Springer, Berlin, 1923, 13–75.Google Scholar
[17] Koszul, J. L., Lectures on Hyperbolic Coxeter Groups. Notes by T. Ochiai. University of Notre Dame, Notre Dame, IN, 1968.Google Scholar
[18] Lannér, F., On complexes with transitive groups of automorphisms. Medd. Lunds Univ. Mat. Sem. 11(1950), 1–71.Google Scholar
[19] Mac Lane, S. and Birkhoff, G., Algebra. Macmillan, New York, and Collier-Macmillan, London, 1967; 3rd edn, Chelsea, New York, 1987.Google Scholar
[20] Magnus, W., Noneuclidean Tesselations and Their Groups. Academic Press, New York-London, 1974.Google Scholar
[21] McMullen, P. and Schulte, E., Constructions for regular polytopes. J. Combin. Theory Ser. A 53(1990), 1–28.Google Scholar
[22] Monson, B. and Weiss, A. I., Polytopes related to the Picard group. Linear Algebra Appl. 218(1995), 185–204.Google Scholar
[23] Monson, B. and Weiss, A. I., Eisenstein integers and related C-groups. Geom. Dedicata 66(1997), 99–117.Google Scholar
[24] Neumann, P. M., Stoy, G. A. and Thompson, E. C., Groups and Geometry. Oxford Univ. Press, Oxford-New York-Tokyo, 1994.Google Scholar
[25] Nostrand, B., Schulte, E. and Weiss, A. I., Constructions of chiral polytopes. Congr. Numer. 97(1993), 165–170.Google Scholar
[26] Picard, É., Sur un groupe des transformations des points de l’espace situés du même côté d’un plan. Bull. Soc. Math. France 12(1884), 43–47, reprinted in OEuvres, t. I (Centre National de la Recherche Scientifique, Paris, 1978), 499–504.Google Scholar
[27] Ratcliffe, J. G., Foundations of Hyperbolic Manifolds. Graduate Texts in Math. 149, Springer-Verlag, New York-Berlin-Heidelberg, 1994.Google Scholar
[28] Schlegel, V., Theorie der homogen zusammengesetzen Raumgebilde. Verh. (=Nova Acte) Kaiserl. Leop.-Carol. Deutsch. Akad. Naturforscher 44(1883), 343–459.Google Scholar
[29] Schulte, E. and Weiss, A. I., Chirality and projective linear groups. Discrete Math. 131(1994), 221–261.Google Scholar
[30] Veblen, O. and Young, J. W., Projective Geometry, Vol. I. Ginn, Boston, 1910; idem, 1916; Blaisdell, New York-Toronto-London, 1965.Google Scholar
[31] Veblen, O. and Young, J. W., Projective Geometry, Vol. II. Ginn, Boston, 1918; Blaisdell, New York-Toronto-London, 1965.Google Scholar