Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T05:30:46.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasiconformal Contactomorphisms and Polynomial Hulls with Convex Fibers

Published online by Cambridge University Press:  20 November 2018

Zoltán M. Balogh  and
Christoph Leuenberger
Zoltán M. Balogh
Affiliation:
Universität Bern, Mathematisches Institut, Sidlerstrasse 5, 3012 Bern, Schweiz email: zoltan@math-stat.unibe.ch
Christoph Leuenberger
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN 47907, U.S.A. email: leuenb@math.purdue.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the polynomial hull of a smoothly varying family of strictly convex smooth domains fibered over the unit circle. It is well-known that the boundary of the hull is foliated by graphs of analytic discs. We prove that this foliation is smooth, and we show that it induces a complex flow of contactomorphisms. These mappings are quasiconformal in the sense of Korányi and Reimann. A similar bound on their quasiconformal distortion holds as in the one-dimensional case of holomorphic motions. The special case when the fibers are rotations of a fixed domain in 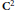${{\text{C}}^{\text{2}}}$ is studied in details.

Keywords

32E2030C65
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 5 , 01 October 1999 , pp. 915 - 935
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Adams, R. A., Sobolev Spaces. Academic Press, 1975.Google Scholar
[2] Astala, K., Area distortion of quasiconformal mappings. Acta. Math. 173(1994), 37–60.Google Scholar
[3] Astala, K., Planar quasiconformal mappings; deformations and interactions. Preprint.Google Scholar
[4] Astala, K., Balogh, Z. and Reimann, M., Lempert Mappings and Holomorphic Motions in Cn. Astérisque (special volume in honor of A. Douady), to appear.Google Scholar
[5] Balogh, Z., Equivariant Contactomorphisms of Circular Surfaces. Houston J. Math., to appear.Google Scholar
[6] Balogh, Z. and Leuenberger, Chr., Higher Dimensional Riemann Maps. Internat. J. Math., to appear.Google Scholar
[7] Bers, L. and Royden, H. L., Holomorphic families of injections. Acta Math. 157(1986), 259–286.Google Scholar
[8] Bland, J., Contact Geometry and CR structures on S3. Acta Math. 172(1994), 1–49.Google Scholar
[9] Bland, J. and Duchamp, T., Moduli for pointed convex domains. Invent.Math. 104(1991), 61–112.Google Scholar
[10] Černe, M., Stationary Discs of Fibrations Over the Circle. Internat. J. Math. 6(1995), 805–823.Google Scholar
[11] Čirca, E. M., Regularity of boundaries of analytic sets. Math. USSR Sb. 45(1983), 291–336.Google Scholar
[12] ForstneriČ, F., Polynomial hulls of sets fibered over the circle. Indiana Univ.Math. J. 37(1988), 869–889.Google Scholar
[13] Garnett, J. B., Bounded Analytic Functions. Academic Press, 1981.Google Scholar
[14] Globevnik, J., Perturbing analytic discs attached to maximal real submanifolds of Cn. Math. Z. 217(1994), 287–316.Google Scholar
[15] Korányi, A. and Reimann, H. M., Quasiconformal mappings on CR manifolds. Lecture Notes in Math. 1422(1990), 59–75.Google Scholar
[16] Korányi, A. and Reimann, H. M., Foundations for the theory for quasiconformal mappings on the Heisenberg group. Adv. Math. 111(1995), 1–87.Google Scholar
[17] Lempert, L., La métrique de Kobayashi et la représentation des domaines sur la boule. Bull. Soc. Math. France 109(1981), 427–474.Google Scholar
[18] Lempert, L., A Precise Result on the Boundary Regularity of Biholomorphic Mappings. Math. Z. 193(1986), 559–579.Google Scholar
[19] Lempert, L., Holomorphic invariants, normal forms, and the moduli space of convex domains. Ann. of Math. 128 (1988), 43–78.Google Scholar
[20] Lempert, L., Erratum: A Precise Result on the Boundary Regularity of Biholomorphic Mappings. Math. Z. 206(1991), 501–504.Google Scholar
[21] Lempert, L., On three-dimensional Cauchy-Riemann manifolds. J. Amer.Math. Soc. 5(1992), 923–969.Google Scholar
[22] Mane´, R., Sad, P. and Sullivan, D., On the dynamics of rational maps. Ann. Sci. École Norm. Sup. 16(1983), 193–217.Google Scholar
[23] Reimann, H. M., Quasiconformal mappings and pseudoconvex domains. Proceedings of the XVIth Rolf Nevanlinna Colloquium, Walter de Gruyter & Co., Berlin-New York, 1996, 191–208.Google Scholar
[24] Semmes, S., A Generalization of Riemann Mappings and Geometric Structures on a Space of Domains in Cn. Mem. Amer. Math. Soc. (472) 98, 1992.Google Scholar
[25] Slodkowski, Z., Polynomial hulls with covex fibers and complex geodesics. J. Funct. Anal. 94(1990), 155–176.Google Scholar
[26] Slodkowski, Z., Holomorphic motions and polynomial hulls. Proc. Amer.Math. Soc. 111(1991), 347–357.Google Scholar
[27] Slodkowski, Z., Extension of holomorphic motions. Ann. Scuola Norm. Sup. Pisa 22(1995), 185–210.Google Scholar
[28] Slodkowski, Z., Canonical model for a class of polynomially convex hulls. Math. Ann. 308(1997), 47–63.Google Scholar
[29] Slodkowski, Z., Personal communication.Google Scholar
[30] Sullivan, D. and Thurston, W., Extending holomorphic motions. Acta. Math. 157(1986) 243–257.Google Scholar
[31] Webster, S. M., On the reflection principle in several complex variables. Proc. Amer. Math. Soc. 71(1978), 26–29.Google Scholar