Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Abadie, Beatriz
and
Exel, Ruy
1997.
Hilbert C*-Bimodules Over Commutative C*-Algebras and an Isomorphism Condition for Quantum Heisenberg Manifolds.
Reviews in Mathematical Physics,
Vol. 09,
Issue. 04,
p.
411.
Kajiwara, Tsuyoshi
Pinzari, Claudia
and
Watatani, Yasuo
1998.
Ideal Structure and Simplicity of theC*-Algebras Generated by Hilbert Bimodules.
Journal of Functional Analysis,
Vol. 159,
Issue. 2,
p.
295.
Schweizer, Jürgen
1999.
A description of Hilbert 𝐶*-modules in which all closed submodules are orthogonally closed.
Proceedings of the American Mathematical Society,
Vol. 127,
Issue. 7,
p.
2123.
Kajiwara, Tsuyoshi
and
Watatani, Yasuo
2000.
Jones index theory by Hilbert C*-bimodules and K-theory.
Transactions of the American Mathematical Society,
Vol. 352,
Issue. 8,
p.
3429.
Ara, Pere
2000.
Morita equivalence and Pedersen ideals.
Proceedings of the American Mathematical Society,
Vol. 129,
Issue. 4,
p.
1041.
Schweizer, Jürgen
2001.
Dilations of C*-Correspondences and the Simplicity of Cuntz–Pimsner Algebras.
Journal of Functional Analysis,
Vol. 180,
Issue. 2,
p.
404.
Kaneda, Masayoshi
and
I. Paulsen, Vern
2004.
Quasi-multipliers of operator spaces.
Journal of Functional Analysis,
Vol. 217,
Issue. 2,
p.
347.
Kodaka, Kazunori
2005.
Partial automorphisms of stable C*-algebras and Hilbert C*-bimodules.
Journal of the Australian Mathematical Society,
Vol. 79,
Issue. 3,
p.
391.
Exel, R.
2007.
Interactions.
Journal of Functional Analysis,
Vol. 244,
Issue. 1,
p.
26.
Hao, Gai
and
Ng, Chi-Keung
2008.
Crossed products of C∗-correspondences by amenable group actions.
Journal of Mathematical Analysis and Applications,
Vol. 345,
Issue. 2,
p.
702.
Abadie, Beatriz
and
Achigar, Mauricio
2009.
Cuntz-Pimsner $C*$-Algebras and Crossed Products by Hilbert $C*$-Bimodules.
Rocky Mountain Journal of Mathematics,
Vol. 39,
Issue. 4,
Ciuperca, A.
and
Elliott, G. A.
2010.
A Remark on Invariants for C*-Algebras of Stable Rank One.
International Mathematics Research Notices,
Skalski, Adam
and
Zacharias, Joachim
2010.
On Approximation Properties of Pimsner Algebras and Crossed Products By Hilbert Bimodules.
Rocky Mountain Journal of Mathematics,
Vol. 40,
Issue. 2,
Heo, Jaeseong
and
Ji, Un Cig
2011.
Quantum stochastic processes for maps on Hilbert C*-modules.
Journal of Mathematical Physics,
Vol. 52,
Issue. 5,
Kwaśniewski, B.K.
2012.
On transfer operators for $C^*$-dynamical systems.
Rocky Mountain Journal of Mathematics,
Vol. 42,
Issue. 3,
Kwaśniewski, B. K.
2013.
Geometric Methods in Physics.
p.
303.
Wang, Chunxiang
2014.
Graded Hilbert C*-modules.
Journal of Mathematical Physics,
Vol. 55,
Issue. 2,
Kwaśniewski, Bartosz Kosma
2014.
Topological freeness for Hilbert bimodules.
Israel Journal of Mathematics,
Vol. 199,
Issue. 2,
p.
641.
Kwaśniewski, B. K.
2014.
Crossed Products for Interactions and Graph Algebras.
Integral Equations and Operator Theory,
Vol. 80,
Issue. 3,
p.
415.
Kang, Sooran
Kumjian, Alex
and
Packer, Judith
2015.
Quantum Heisenberg manifolds as twisted groupoidC⁎-algebras.
Journal of Mathematical Analysis and Applications,
Vol. 425,
Issue. 2,
p.
1039.
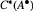 , the enveloping C*-algebra of the C*-algebraA with its product perturbed by a positive quasi-multiplier
, the enveloping C*-algebra of the C*-algebraA with its product perturbed by a positive quasi-multiplier 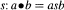 , is isomorphic to the closure
, is isomorphic to the closure 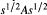 (Proposition 3.1). Section 4 contains the main theorem (4.3), and in Section 5 we explain the analogy with the relative position of two subspaces of a Hilbert spaces and present some complements.
(Proposition 3.1). Section 4 contains the main theorem (4.3), and in Section 5 we explain the analogy with the relative position of two subspaces of a Hilbert spaces and present some complements.

