Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T14:39:48.707Z Has data issue: false hasContentIssue false
  • English
  • Français

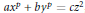Quelques résultats sur les équations $a{{x}^{p}}\,+\,b{{y}^{p}}\,=\,c{{z}^{2}}$

Published online by Cambridge University Press:  20 November 2018

W. Ivorra  and
A. Kraus
W. Ivorra
Affiliation:
Institut de Mathématiques, Université Paris VI, Équipe de Théorie des Nombres, UMR 7586 du CNRS, 175 Rue du Chevaleret, Paris 75013, France e-mail: ivorra@math.jussieu.fr, e-mail: kraus@math.jussieu.fr
A. Kraus
Affiliation:
Institut de Mathématiques, Université Paris VI, Équipe de Théorie des Nombres, UMR 7586 du CNRS, 175 Rue du Chevaleret, Paris 75013, France e-mail: ivorra@math.jussieu.fr, e-mail: kraus@math.jussieu.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

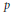Let $p$ be a prime number ≥ 5 and 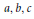$a,\,b,\,c$ be non zero natural numbers. Using the works of K. Ribet and A. Wiles on the modular representations, we get new results about the description of the primitive solutions of the diophantine equation 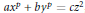$a{{x}^{p}}\,+\,b{{y}^{p}}\,=\,c{{z}^{2}}$, in case the product of the prime divisors of 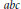$abc$ divides 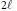$2\ell $, with 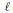$\ell $ an odd prime number. For instance, under some conditions on 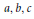$a,\,b,\,c$, we provide a constant 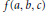$f(a,\,b,\,c)$ such that there are no such solutions if 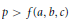$p\,>\,f(a,\,b,\,c)$. In application, we obtain information concerning the 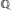$\mathbb{Q}$-rational points of hyperelliptic curves given by the equation 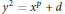${{y}^{2}}\,=\,{{x}^{p}}\,+\,d$ with 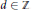$d\,\in \,\mathbb{Z}$.

Keywords

11G
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 1 , 01 February 2006 , pp. 115 - 153
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Atkin, A. O. L. et Lehner, J., Hecke operators on Γ0(m). Math. Ann. 185(1970), 134–160.Google Scholar
[2] Batut, C., Bernardi, D., Belabas, K., Cohen, H., et Olivier, M., User's guide to PARI-GP (version 2.0.12). Lab A2X, Université de Bordeaux I, Bordeaux, 1998.Google Scholar
[3] Bennett, M. A. and Skinner, C. M., Ternary Diophantine equations via Galois representations and modular forms. Canad. J. Math. 56(2004), 23–54.Google Scholar
[4] Beukers, F., On the generalized Ramanujan-Nagell equation. I. Acta Arith. 38(1981), 389–410.Google Scholar
[5] Breuil, C., Conrad, B., Diamond, F., et Taylor, R., On the modularity of elliptic curves over ℚ : wild 3-adic exercises.. J. Amer. Math. Soc. 14(2001), 843–939.Google Scholar
[6] Cohn, J. H. E., The diophantine equation x.2 + 3 = yn. Glasgow Math. J. 35(1993), 203–206 Google Scholar
[7] Cremona, J. E., Algorithms for modular elliptic curves. Second edition, Cambridge University Press, Cambridge, 1997.Google Scholar
[8] Cremona, J. E., Elliptic curves data, disponible à : http://www.maths.nott.ac.uk/personal/jec/ftp/data/ Google Scholar
[9] Darmon, H., The equations xn + yn = z2 and xn + yn = z3 . Intern. Math. Res. Notices 10(1993), 263–274.Google Scholar
[10] Darmon, H., Serre's conjectures. CMS Conf. Proc. 17, American Mathematical Society, Providence, RI, 1995 pp. 135–153.Google Scholar
[11] Darmon, H. et Granville, A., On the equations zm = F(x, y) and Axp + Byq = Czr . Bull. London Math. Soc. 27(1995), 513–543.Google Scholar
[12] Darmon, H. et Merel, L., Winding quotients and some variants of Fermat's last theorem. J. Reine Angew. Math. 490(1997), 81–100.Google Scholar
[13] Frey, G., Links between stable elliptic curves and certain Diophantine equations. Ann. Univ. Sarav. Ser. Math. 1(1986), 1–40.Google Scholar
[14] Halberstadt, E. et Kraus, A., Sur les modules de torsion des courbes elliptiques. Math. Ann. 310(1998), 47–54.Google Scholar
[15] Halberstadt, E. et Kraus, A., Courbes de Fermat : résultats et problèmes. J. Reine Angew. Math. 548(2002), 167–234.Google Scholar
[16] Halberstadt, E., manuscrit (2003).Google Scholar
[17] Ivorra, W., Sur les équations xp + 2β yp = z2 . et xp + 2β yp = 2z2 . Acta. Arith. 108(2003), 327–338.Google Scholar
[18] Ivorra, W., Courbes elliptiques sur ℚ, ayant un point d’ordre 2 rationnel sur ℚ, de conducteur 2 N p. Dissertationes Math. 429(2004).Google Scholar
[19] Ivorra, W., équations diophantiennes ternaires de type (p, p, 2) et courbes elliptiques, Chap. IV, Thèse Université Paris VI, 2004.Google Scholar
[20] Kenku, M. A., On the number of ℚ-isomorphism classes of elliptic curves in each ℚ-isogeny class. J. Number Theory 15(1982), 199–202.Google Scholar
[21] Kraus, A., Sur le défaut de semi-stabilité des courbes elliptiques à réduction additive. Manuscripta Math. 69(1990), 353–385.Google Scholar
[22] Kraus, A., Détermination du poids et du conducteur associés aux représentations des points de p-torsion d’une courbe elliptique. Dissertationes Math. 364(1997).Google Scholar
[23] Kraus, A., Sur l’équation Lap + bp = c2 . Huitièmes rencontres arithmétiques de Caen, Université de Caen, 6-7 juin 1997.Google Scholar
[24] Kraus, A., Majorations effectives pour l’équation de Fermat généralisée. Canad. J. Math. 49(1997), 1139–1161.Google Scholar
[25] Kraus, A., Sur l’équation a3 + b 3 = cp. Experiment. Math. 7(1998), 1–13.Google Scholar
[26] Kraus, A., Une question sur les équations xm – ym = Rzn. Compositio Math. 132(2002), 1–26.Google Scholar
[27] Kraus, A. et Oesterlé, J., Sur une question de B. Mazur. Math. Ann. 293(1992), 259–275.Google Scholar
[28] Lesage, J.-L., Différence entre puissances et carrés d’entiers. J. Number Theory 73(1998), 390–425.Google Scholar
[29] Ligozat, G., Courbes modulaires de genre 1. Bull. Soc. Math. France 43(1975).Google Scholar
[30] Mazur, B., Rational isogenies of prime degree. Invent. Math. 44(1978), 129–162.Google Scholar
[31]Metmod, disponible à : http://www.math.jussieu.fr/∽ivorra. Google Scholar
[32] Momose, F., Rational points on the modular curves X split (p). Compositio Math. 52(1984), 115–137.Google Scholar
[33] Papadopoulos, I., Sur la classification de Néron des courbes elliptiques en caractéristique résiduell. 2 et 3. J. Number Theory 44(1993), 119–152.Google Scholar
[34] Poonen, B., Some Diophantine equations of the form xn + yn = zm. Acta Arith. 86(1998), 193–205.Google Scholar
[35] Ribet, K., On modular representations of Gal $ $ arising from modular forms. Invent.Math. 100(1990), 431–476.Google Scholar
[36] Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques. Invent.Math. 15(1972), 259–331.Google Scholar
[37] Serre, J.-P., Sur les représentations modulaires de degré 2 d $ $ . Duke Math. J. 54(1987), 179–230.Google Scholar
[38] Serre, J.-P., Travaux de Wiles (et Taylor,…). I. . Séminaire Bourbaki 1994/95, Astérisque 237(1996) 319–332.Google Scholar
[39] Setzer, B., Elliptic curves of prime conductor. J. London Math. Soc. (2) 10(1975), 367–378.Google Scholar
[40] Silverman, J., The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics 106, Springer-Verlag, 1986.Google Scholar
[41] Stein, W., Modular forms database, disponible à l’adresse: http://modular.fas.harvard.edu/Tables/Google Scholar
[42] Tate, J., Algorithm for determining the type of a singular fiber in an elliptic pencil. In: Modular Functions of One Variable IV, Lecture Notes in Math. 476, Springer, Berlin, 1975, pp. 33–52.Google Scholar
[43] Wiles, A., Modular elliptic curves and Fermat's last theorem. Ann. of Math. (2) 141(1995), 443–551.Google Scholar