Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T10:23:04.585Z Has data issue: false hasContentIssue false
  • English
  • Français

The Radius of Convexity of a Linear Combination of Functions in 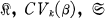or uα

Published online by Cambridge University Press:  20 November 2018

Douglas Michael Campbell
Douglas Michael Campbell*
Affiliation:
Brigham Young University, Provo, Utah
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Labelle and Rahman [4] showed that if f , g ∈ 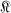, the normalized convex functions in the unit disc D, then has a radius of convexity at least as large as the smallest root of 1 – 3r + 2r2 — 2r3 = 0. Their method requires neither the properties of the arithmetic mean nor the strong geometric properties of 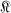; indeed, the procedure works for a linear combination of functions from any linear invariant family of finite order.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 25 , Issue 5 , October 1973 , pp. 982 - 985
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Campbell, D. M., Locally univalent functions with locally univalent derivatives, Trans. Amer. Math. Soc. 162 (1971), 395–409.Google Scholar
2. Campbell, D. M., β-close-to-bounded boundary rotation functions I. (to appear).Google Scholar
3. Goluzin, G. M., Geometric theory of functions of a complex variable, Amer. Math. Soc. Vol. 26 (Providence, R. I., 1969).Google Scholar
4. Labelle, G. and Rahman, Q. I., Remarque sur la moyenne arithmétique de fonctions univalentes convexes, Can. J. Math. 21 (1969), 977–981.Google Scholar
5. Pommerenke, C., Linear-invariante Familien Analytischer Funktionen. I, Math. Ann. 155 (1964), 108–154.Google Scholar