Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ramanathan, K G
1980.
Ramanujan and the congruence properties of partitions.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 89,
Issue. 3,
Gordon, B.
and
Hughes, K.
1981.
Analytic Number Theory.
Vol. 899,
Issue. ,
p.
333.
Gordon, Basil
1983.
Ramanujan congruences for p-k (mod 11').
Glasgow Mathematical Journal,
Vol. 24,
Issue. 2,
p.
107.
Garvan, F. G.
1984.
A simple proof of Watson's partition congruences for powers of 7.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 36,
Issue. 3,
p.
316.
Gordon, Basil
and
Sinor, Dale
1989.
Number Theory, Madras 1987.
Vol. 1395,
Issue. ,
p.
173.
Garvan, Frank
2001.
The Andrews Festschrift.
p.
111.
Boylan, Matthew
2003.
Exceptional congruences for the coefficients of certain eta-product newforms.
Journal of Number Theory,
Vol. 98,
Issue. 2,
p.
377.
Andrews, George E.
2008.
Surveys in Number Theory.
Vol. 17,
Issue. ,
p.
1.
BARUAH, NAYANDEEP DEKA
and
OJAH, KANAN KUMARI
2011.
SOME CONGRUENCES DEDUCIBLE FROM RAMANUJAN'S CUBIC CONTINUED FRACTION.
International Journal of Number Theory,
Vol. 07,
Issue. 05,
p.
1331.
Chen, William Y. C.
and
Lin, Bernard L. S.
2011.
Congruences for bipartitions with odd parts distinct.
The Ramanujan Journal,
Vol. 25,
Issue. 2,
p.
277.
Andrews, George E.
and
Berndt, Bruce C.
2012.
Ramanujan's Lost Notebook.
p.
181.
Berndt, Bruce C.
Gugg, Chadwick
and
Kim, Sun
2012.
Partitions, q-Series, and Modular Forms.
Vol. 23,
Issue. ,
p.
13.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
13.
Lazarev, Oleg
and
Swisher, Holly
2012.
A Combinatorial Proof of a Recursive Formula for Multipartitions.
Integers,
Vol. 12,
Issue. 1,
Baruah, Nayandeep Deka
and
Sarmah, Bipul Kumar
2013.
Identities and congruences for the general partition and Ramanujan’s tau functions.
Indian Journal of Pure and Applied Mathematics,
Vol. 44,
Issue. 5,
p.
643.
Garvan, F. G.
2013.
Number Theory and Related Fields.
Vol. 43,
Issue. ,
p.
165.
Lin, Bernard L.S.
2014.
Some results on bipartitions with 3-core.
Journal of Number Theory,
Vol. 139,
Issue. ,
p.
44.
Huber, Tim
2014.
A theory of theta functions to the quintic base.
Journal of Number Theory,
Vol. 134,
Issue. ,
p.
49.
Belmont, Eva
Lee, Holden
Musat, Alexandra
and
Trebat-Leder, Sarah
2014.
$$\ell $$ ℓ -Adic properties of partition functions.
Monatshefte für Mathematik,
Vol. 173,
Issue. 1,
p.
1.
Chen, William Y. C.
Du, Daniel K.
Hou, Qing-Hu
and
Sun, Lisa H.
2014.
Congruences of multipartition functions modulo powers of primes.
The Ramanujan Journal,
Vol. 35,
Issue. 1,
p.
1.

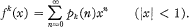
 ; unfortunately his results are incorrect, because of an error in his Lemma 4 on which his main theorems depend. This error is essentially a misquotation of the results of Watson (5), which one may readily understand in view of Watson's formidable notation.
; unfortunately his results are incorrect, because of an error in his Lemma 4 on which his main theorems depend. This error is essentially a misquotation of the results of Watson (5), which one may readily understand in view of Watson's formidable notation.

