Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Harnad, J.
and
McKay, J.
2000.
Modular solutions to equations of generalized Halphen type.
Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,
Vol. 456,
Issue. 1994,
p.
261.
Kim, Chang Heon
and
Koo, Ja Kyung
2002.
Self-recursion formulas of certain monstrous functions.
Journal of Pure and Applied Algebra,
Vol. 171,
Issue. 1,
p.
27.
Kang, Seok-Jin
Kim, Chang Heon
Koo, Ja Kyung
and
Oh, Young-Tak
2005.
Graded Lie superalgebras and super-replicable functions.
Journal of Algebra,
Vol. 285,
Issue. 2,
p.
531.
McKay, John
and
Sebbar, Abdellah
2007.
Frontiers in Number Theory, Physics, and Geometry II.
p.
373.
Scheithauer, Nils R.
2008.
Generalized Kac-Moody algebras, automorphic forms and Conway's group II.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2008,
Issue. 625,
Carnahan, Scott
2017.
Fricke Lie algebras and the genus zero property in Moonshine.
Journal of Physics A: Mathematical and Theoretical,
Vol. 50,
Issue. 40,
p.
404002.
DeHority, Samuel
Gonzalez, Xavier
Vafa, Neekon
and
Van Peski, Roger
2018.
Moonshine for all finite groups.
Research in the Mathematical Sciences,
Vol. 5,
Issue. 1,
Plazas, Jorge
2019.
Noncommutative Geometry of Groups Like Γ0(N).
p-Adic Numbers, Ultrametric Analysis and Applications,
Vol. 11,
Issue. 1,
p.
61.
Heim, Bernhard
and
Murase, Atsushi
2019.
Completely replicable functions and symmetries.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 89,
Issue. 2,
p.
169.
Duncan, John F. R.
Harvey, Jeffrey A.
and
Rayhaun, Brandon C.
2024.
Modular Products and Modules for Finite Groups.
Algebras and Representation Theory,
Vol. 27,
Issue. 1,
p.
115.


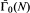 with finite index and
with finite index and 