Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T14:59:18.440Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational Solutions of Painlevé Equations

Published online by Cambridge University Press:  20 November 2018

Yuan Wenjun  and
Li Yezhou
Yuan Wenjun
Affiliation:
Department of Mathematics, Guihuagang School District, Guangzhou University, Guangzhou 510405, P. R. China, and Institute of Mathematics Academy of Mathematics and System Sciences, Academia Sinica, Beijing 100080, P. R. China
Li Yezhou
Affiliation:
Institute of Mathematics, Academy of Mathematics and System Sciences, Academia Sinica, Beijing 100080, P. R. China and School of Sciences, Beijing University of Posts and Telecommunications, Beijing 100876, P. R. China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the sixth Painlevé equation 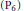$({{\text{P}}_{6}})$ below where 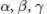$\alpha ,\beta ,\gamma$ and 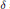$\delta$ are complex parameters. We prove the necessary and sufficient conditions for the existence of rational solutions of equation 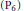$({{\text{P}}_{6}})$ in term of special relations among the parameters. The number of distinct rational solutions in each case is exactly one or two or infinite. And each of them may be generated by means of transformation group found by Okamoto [7] and Bäcklund transformations found by Fokas and Yortsos [4]. A list of rational solutions is included in the appendix. For the sake of completeness, we collected all the corresponding results of other five Painlevé equations 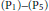$({{\text{P}}_{1}})-({{\text{P}}_{5}})$ below, which have been investigated by many authors [1]–[7].

Keywords

30D3534A20Painlevé differential equationrational functionBäcklund transformation
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 3 , 01 June 2002 , pp. 648 - 670
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Airault, H., Rational solutions of Painlevé equations. Stud. Appl. Math. 61 (1979), 31–53.Google Scholar
[2] Erugin, N. P., The analytic theory and problems of the real theory of differential equations connected with the first method and with the methods of the analytic theory. Differential Equations 3 (1967), 943–966.Google Scholar
[3] Fokas, A. S. and Ablotz, M. J., On a unified approach to transformations and elementary solutions of Painlevé equations. J. Math. Phys. 23 (1982), 2033–2042.Google Scholar
[4] Fokas, A. S. and Yortsos, Y. C., The transformation properties of the sixth Painlevé equation and one-parameter families of solutions. Lett. Nuovo Cimento 30 (1981), 539–544.Google Scholar
[5] Gromak, V. I. and Lukashevich, N. A., Analytic properties of solutions of the Painlevé equations. Universitetskoe,Minsk, 1990, 1–157 (in Russian).Google Scholar
[6] Iwasaki, K., Kimura, H., Shimomura, S. and Yoshida, M., From Gauss to Painlevé. Vieweg, Braunschweig, 1991.Google Scholar
[7] Kitaev, A. V., Law, C. K. and McLeod, J. B., Rational solutions of the fifth Painlevé equation. Preprint.Google Scholar
[8] Okamoto, K., Studies of the Painlevé equations. Math. Ann. 275 (1986), 221–255.Google Scholar