Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T08:47:13.803Z Has data issue: false hasContentIssue false
  • English
  • Français

Ray Sequences of Best Rational Approximants For |x|α

Published online by Cambridge University Press:  20 November 2018

E. B. Saff  and
H. Stahl
E. B. Saff
Affiliation:
Institute for Constructive Mathematics Department of Mathematics University of South Florida Tampa, Florida 33620 U.S.A.
H. Stahl
Affiliation:
TFH/FB2 Luxemburger Str. 10 D-1000 Berlin 65 Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The convergence behavior of best uniform rational approximations 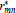with numerator degree m and denominator degree n to the function |x|α, α > 0, on [-1, 1] is investigated. It is assumed that the indices (m, n) progress along a ray sequence in the lower triangle of the Walsh table, i.e. the sequence of indices {(m, n)} satisfies

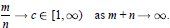
In addition to the convergence behavior, the asymptotic distribution of poles and zeros of the approximants and the distribution of the extreme points of the error function 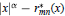on [-1, 1] will be studied. The results will be compared with those for paradiagonal sequences (m = n + 2[α/2]) and for sequences of best polynomial approximants.

Keywords

41A2541A44Walsh tablerational approximationbest approximationdistribution of poles and zeros
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 49 , Issue 5 , 01 October 1997 , pp. 1034 - 1065
Copyright
Copyright © Canadian Mathematical Society 1997

References

[An] Anderson, J.-E., Rational approximation to functions like xα in integral norms, Anal. Math. 14(1988), 11–25.Google Scholar
[Be1] Bernstein, S., About the best approximation of |x|p by means of polynomials of very high degree, (Russian), Collected Works II(1938), 262–272.Google Scholar
[Be2] Bernstein, S., Sur meilleure approximation de |x. par des polynômes degrés donnés, Acta Math. 37(1913), 1–57.Google Scholar
[BIS] Blatt, H.-P., Iserles, A. and Saff, E.B., Remarks on the behavior of zeros and poles of best approximating polynomials and rational functions. In: Algorithms for Approximation, (eds. Mason, J.C. and Cox, M.G.), Inst. Math. Appl. Conf. Ser. New Ser. 10, Claredon Press, Oxford, 1987. 437–445.Google Scholar
[BS] Blatt, H.-P. and Saff, E.B., Behavior of zeros of polynomials of near best approximation, J.Approx. Theory 46(1986), 323–344.Google Scholar
[Bu1] Bulanow, A.P., Asymptotics for the least derivation of |x. from rational functions, Mat. Sb. (118) 76(1968), 288–303. English transl. in Math. USSR-Sb. 5(1968), 275–290.Google Scholar
[Bu2] Bulanow, A.P., The approximation of x1/3 by rational functions, (Russian), Vests¯ı Akad. Navuk Belarus¯ı Ser. F¯ız. Mat. Navuk 2(1968), 47–56.Google Scholar
[FrSz] Freud, G. and Szabados, J., Rational approximation to xα, ActaMath. Acad. Sci. Hungar. 18(1967), 393.Google Scholar
[Ga] Ganelius, T., Rational approximation to x α on [0, 1], Anal. Math. 5(1979), 19–33.Google Scholar
[Ge] Gelfond, A.O., Differenzenrechnung. Deutscher Verlag der Wissenschaften, Berlin, 1958.Google Scholar
[Go1] Gonchar, A.A., On the speed of rational approximation of continuous functions with characteristic singularities, Mat. Sb. (115) 73(1967), 630–638. English transl. in Math. USSR-Sb. 2(1967).Google Scholar
[Go2] Gonchar, A.A., Rational approximation of the function xα. (Russian), In: Constructive Theory of Functions, Proc. Internat. Conf, Varna, 1970. Izdat. Bolgar. Akad. Nauk, Sofia, 1972. 51–53.Google Scholar
[Go3] Gonchar, A.A., The rate of rational approximation and the property of single-valuedness of an analytic function in a neighborhood of an isolated singular point, Mat. Sb. (136) 94(1974), 265–282. English transl. in Math. USSR-Sb. 23(1974).Google Scholar
[Ka] Kadec, M.I., On the distribution of points of maximum deviation in the approximation of continuous functions by polynomials, Amer. Math. Soc. Transl. (2) 26(1963), 231–234.Google Scholar
[KaSt] Karlin, S. and Studden, W.J., Tchebycheff Systems: With Applications in Analysis and Statistics. Interscience Publishers, New York, 1966.Google Scholar
[La] Landkof, N.S., Foundations of Modern Potential Theory. GrundlehrenMath.Wiss. 190, Springer-Verlag, New York, 1972.Google Scholar
[Me] Meinardus, G., Approximation of Functions: Theory and NumericalMethods. Springer-Verlag,NewYork, 1967.Google Scholar
[Ne] Newman, D.J., Rational approximation to |x|, Michigan Math. J. 11(1964), 11–14.Google Scholar
[Ri] Rivlin, T.J., An Introduction to the Approximation of Functions. Blaisdell Publ. Co., Waltham, Massachusetts, 1969.Google Scholar
[Sa] Saff, E.B., A principle of contamination in best polynomial approximation. In: Approximation and Optimization, Lecture Notes in Math. 1354, (eds. Gomez, Guerra, Jimeniz and Lopez), Springer-Verlag, Berlin, 1988. 79–97.Google Scholar
[SaSt1] Saff, E.B. and Stahl, H., Sequences in the Walsh table for xα. In: Constructive Theory of Functions, (eds. Ivanov, K., Petrushev, P. and Bl. Sendov), Bulgarian Academy of Science, Sofia, 1992. 249–259.Google Scholar
[SaSt2] Saff, E.B., Asymptotic distribution of poles and zeros of best rational approximants for |x|α, Proc. of the Semester of Funct. Theory at the Internat. Banach Center, Warsaw, 1992. to appear.Google Scholar
[St1] Stahl, H., Best uniform rational approximation of |x| on [-1, 1], Mat. Sb. (8) 183, 85–118.Google Scholar
[St2] Stahl, H., Best uniform rational approximation of xα on [0, 1], Bull. Amer.Math. Soc. 28(1993), 116–122.Google Scholar
[StTo] Stahl, H. and Totik, V., General Orthogonal Polynomials. Encyclopedia Math. Appl. 43, Cambridge University Press, 1992.Google Scholar
[Ts] Tsuji, M., Potential Theory in Modern Function Theory. Maruzen, Tokyo, 1959.Google Scholar
[Tz] Tzimbalario, J., Rational approximation to x α, J. Approx. Theory 16(1976), 187–193.Google Scholar
[VC1] Varga, R.S. and Carpenter, A.J., On the Bernstein conjecture in approximation theory, Constr. Approx. 1(1985), 333–348. Russian transl. in Mat. Sb. (171) 129(1986), 535–548.Google Scholar
[VC2] Varga, R.S., Some numerical results on best uniform rational approximation of xα on [0, 1], Numer. Algorithms, to appear.Google Scholar
[VC3] Varga, R.S., Some numerical results on best uniform polynomial approximation of xα on [0, 1]. In: Methods of Approximation Theory in Complex Analysis and Mathematical Physics, (eds. Gonchar, A.A. and Saff, E.B.), Moskow, “Nauka”, 1992. 192–222.Google Scholar
[VRC] Varga, R.S., Ruttan, A. and Carpenter, A.J., Numerical results on best uniform rational approximation of |x. on [-1, 1], Mat. Sb. (11) 182(1991), 1523–1541.Google Scholar
[Vj1] Vjacheslavov, N.S., On the approximation of xα by rational functions, Izv. Akad. Nauk-USSR 44(1980); English transl. in Math. USSR-Izv. 16(1981), 83–101.Google Scholar
[Vj2] Vjacheslavov, N.S., On the uniform approximation of |x. by rational functions, Dokl. Akad. Nauk SSSR 220(1975), 512–515. English transl. in Soviet Math. Dokl. 16(1975), 100–104.Google Scholar
[Vj3] Vjacheslavov, N.S., The approximation of|x. by rational functions, (Russian), Mat. Zametki 16(1974), 163–171.Google Scholar