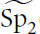Reducibility of the Principal Series for (F) over a p-adic Field

Abstract

Let 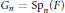${{G}_{n}}=\text{S}{{\text{p}}_{n}}\left( F \right)$ be the rank 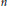$n$ symplectic group with entries in a nondyadic 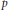$p$-adic field $F$. We further let ${{\tilde{G}}_{n}}$ be the metaplectic extension of 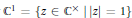${{G}_{n}}\,\text{by}\,{{\mathbb{C}}^{1}}=\left\{ z\in {{\mathbb{C}}^{\times }}|\,|z|=1 \right\}$ defined using the Leray cocycle. In this paper, we aim to demonstrate the complete list of reducibility points of the genuine principal series of 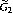${{\tilde{G}}_{2}}$. In most cases, we will use some techniques developed by Tadić that analyze the Jacquet modules with respect to all of the parabolics containing a fixed Borel. The exceptional cases involve representations induced from unitary characters 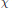$\chi $ with 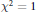${{\chi }^{2}}=1$. Because such representations $\pi $ are unitary, to show the irreducibility of $\pi $, it suffices to show that 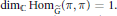${{\dim}_{\mathbb{C}}}\,\text{Ho}{{\text{m}}_{{\tilde{G}}}}\left( \pi ,\,\pi \right)\,=\,1$ . We will accomplish this by examining the poles of certain intertwining operators associated to simple roots. Then some results of Shahidi and Ban decompose arbitrary intertwining operators into a composition of operators corresponding to the simple roots of 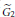${{\tilde{G}}_{2}}.$ We will then be able to show that all such operators have poles at principal series representations induced from quadratic characters and therefore such operators do not extend to operators in 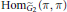$\text{Ho}{{\text{m}}_{{{{\tilde{G}}}_{2}}}}\left( \pi ,\,\pi \right)$ for the $\pi $ in question.