Reflection of Willmore Surfaces with Free Boundaries

Abstract

We study immersed surfaces in ${\mathbb R}^3$ that are critical points of the Willmore functional under boundary constraints. The two cases considered are when the surface meets a plane orthogonally along the boundary and when the boundary is contained in a line. In both cases we derive weak forms of the resulting free boundary conditions and prove regularity by reflection.

1 Introduction

This note is concerned with Willmore surfaces under free boundary conditions. Let $\Sigma $ be an oriented, two-dimensional manifold with boundary $\partial \Sigma $ . For a smooth immersion $f\colon \Sigma \to {\mathbb R}^3,$ the Willmore functional is defined by

(1.1) $$ \begin{align} {\mathcal W}(\,f) = \frac{1}{4} \int_\Sigma H^2\,d\mu_g. \end{align} $$

Here, $\mu _g$ is the measure associated with the induced Riemannian metric g, and H is the mean curvature with respect to the unit normal $\nu \colon \Sigma \to {\mathbb S}^2$ . We denote by h the second fundamental form of f and put $h^\circ = h - \frac {1}{2} H g$ . Let $f(\cdot,t)$ be a smooth variation with velocity field $\phi = \varphi \nu + Df \cdot \xi $ . The first variation is (see [13, 1]),

(1.2) $$ \begin{align} \frac{d}{dt} {\mathcal W}(\,f(\cdot,t))|_{t=0} = \frac{1}{2} \int_\Sigma W(\,f) \varphi\,d\mu_g + \frac{1}{2} \int_{\partial \Sigma} \omega(\eta)\,ds_g, \end{align} $$

where $\eta $ denotes the interior unit normal along $\partial \Sigma $ with respect to g, and

(1.3) $$ \begin{align} W(\,f) & = \Delta_g H + |h^\circ|^2 H, \end{align} $$

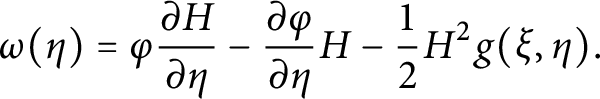(1.4) $$ \begin{align} \omega(\eta) & = \varphi \frac{\partial H}{\partial \eta} - \frac{\partial \varphi}{\partial \eta} H - \frac{1}{2} H^2 g(\xi,\eta). \end{align} $$

In this paper, we address two free boundary situations. First, for a given support surface $S,$ we consider the class of smooth immersions $\widetilde {\mathcal M}(S)$ that meet S orthogonally along the boundary $\partial \Sigma $ . The admissible variations $\phi \in T_f{\widetilde {\mathcal M}}(S)$ are characterized by the equations

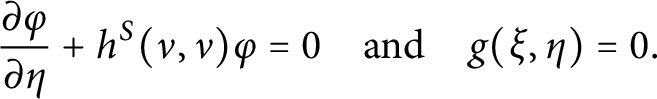(1.5) $$ \begin{align} \frac{\partial \varphi}{\partial \eta} + h^S(\nu,\nu) \varphi = 0\quad \text{and}\quad g(\xi,\eta) = 0. \end{align} $$

For immersions f that are critical in that class, Alessandroni and the first author computed in [1] the following natural boundary condition

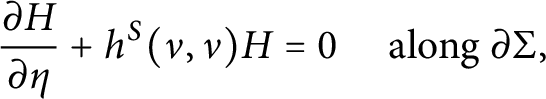(1.6) $$ \begin{align} \frac{\partial H}{\partial \eta} + h^S(\nu,\nu) H = 0 \quad \mbox{ along }\partial \Sigma, \end{align} $$

where $h^S$ is the second fundamental form of $S \subset {\mathbb R}^3$ .

Secondly, we consider immersions that are confined to a given support curve $\Gamma \subset {\mathbb R}^3$ along the boundary, but without prescribing the tangent plane along $\partial \Sigma $ . In this case, the critical immersions in the corresponding class satisfy

(1.7) $$ \begin{align} H = 0 \quad \mbox{ along } \partial \Sigma. \end{align} $$

This is referred to as Navier boundary condition in [5]. Our note deals with the cases of a plane S and a line $\Gamma $ , proving reflection principles in both situations. For the plane, the result is due to J. C. C. Nitsche, assuming $C^{4,\nu }$ regularity up to the boundary [12]. We extend Nitsche’s theorem to a weak setting, and further adapt our arguments to the case of a line $\Gamma $ .

The class of $W^{2,2}$ (Lipschitz) immersions on an open set $U \subset {\mathbb R}^2$ is defined by

(1.8) $$ \begin{align} W^{2,2}_{\mathrm{imm}}(U,{\mathbb R}^3) = \{\,f \in W^{2,2} \cap W^{1,\infty}(U,{\mathbb R}^3): {\mathrm{ess\,inf\,}} (\det g)> 0\}. \end{align} $$

This is an open subset of $W^{2,2}\cap W^{1,\infty }(U,{\mathbb R}^3)$ . We remark that the $W^{2,2}$ conformal immersions $W^{2,2}_{\mathrm {conf}}(U,{\mathbb R}^3)$ introduced in [7] are exactly those $f \in W^{2,2}_{\mathrm {imm}}(U,{\mathbb R}^3)$ satisfying $g_{11} = g_{22}$ and $g_{12} = 0$ . In other words, we have $g_{ij} = e^{2u} \delta _{ij}$ where $u \in W^{1,2} \cap L^\infty (U)$ . In the sequel we let $Q = (-\pi,\pi ) \times (-1,1)$ , $I = (-\pi,\pi ) \times \{0\} =: (-\pi,\pi )$ and $Q_{\pm } = \{(x,y) \in Q: {\pm } y> 0\}$ . The precise choice of Q will be convenient in the appendix.

Theorem Let ${\mathcal M}$ be the class of $f \in W^{2,2}_{\mathrm {imm}}(Q_{+},{\mathbb R}^3)$ satisfying the constraints

(1.9) $$ \begin{align} f_3 & = 0 \quad \mbox{ along }I, \end{align} $$

(1.10) $$ \begin{align} \langle \nu, e_3 \rangle & = 0 \quad \mbox{ along }I \mbox{ almost everywhere.} \end{align} $$

Assume that $f \in W^{2,2}_{\mathrm {conf}}(Q_{+},{\mathbb R}^3)$ is a critical point of the Willmore energy for variations in ${\mathcal M}$ with compact support in $Q_{+} \cup I$ . Then extending f to Q by

$$\begin{align*}f\colon Q_{-} \longrightarrow {\mathbb R}^3,\,f(x,y) = \big(\,f_1(x,-y),f_2(x,-y),-f_3(x,-y)\big), \end{align*}$$

yields a smooth Willmore immersion $f \in C^\infty (Q,{\mathbb R}^3)$ .

The key tool of the proof is the interior regularity theorem of Rivière [14], which directly implies regularity on $Q_{+}$ (and on $Q_{-}$ ). We show that f is of class $W^{2,2}_{\mathrm {conf}}(Q,{\mathbb R}^3)$ and solves the weak Willmore equation on all of Q, so that [14] applies. For the second free boundary problem where f is critical among immersions mapping I into a line the arguments are quite analogous. The extension by reflection across the line again gives a smooth Willmore immersion; see Theorem 4.2 in Section 4.

The notion of critical point used in Theorem 1 is that the first variation $\delta {\mathcal W}(\,f,\phi )$ vanishes for all admissible vector fields $\phi $ . Here admissible means that $\phi $ is formally a tangent vector to ${\mathcal M}$ at f,i.e., it satisfies the equations obtained by linearizing the constraints (1.9) and (1.10) at the immersion $f \in {\mathcal M}$ (clearly only (1.10) is non-linear). We prove in Section 3 that, locally, any admissible vector field $\phi $ is indeed the tangent vector of a curve in ${\mathcal M}$ at f. Therefore, our regularity result would apply, for example, to show the regularity of minimizers.

In the case where the curve and the tangent plane are prescribed along the boundary, there are substantial existence and regularity results for minimizers by Schätzle [15] and Da Lio, Palmurella, and Rivière [4]. It is clearly of interest to develop an analogous theory for the free boundary problems in the case of curved supporting surfaces or curves.

Due to its conformal invariance, it is also interesting to study the corresponding problem for the functional

$$\begin{align*}{\mathcal T}(\,f) = \frac{1}{2} \int_\Sigma |h^\circ|^2\,d\mu_g. \end{align*}$$

In Section $5,$ we calculate the first variation of ${\mathcal T}$ to be

(1.11) $$ \begin{align} \frac{d}{dt} {\mathcal T}(\,f(\cdot,t))|_{t=0} = \frac{1}{2} \int_\Sigma W(\,f) \varphi\,d\mu_g + \int_{\partial \Sigma} \alpha(\eta)\,ds_g, \end{align} $$

where $W(\,f)$ and the smooth variation $f(\cdot,t)$ are as above, and

(1.12) $$ \begin{align} \alpha(\eta) = \frac12 \varphi \frac{\partial H}{\partial \eta} - h^\circ(\mathrm{grad} \varphi,\eta)-\frac12 |h^\circ|^2g(\xi,\eta). \end{align} $$

We consider again the free boundary problem when the immersions meet S orthogonally along the boundary $\partial \Sigma $ . In the case of the support surface S being a plane, the boundary condition is again given by

$$\begin{align*}\frac{\partial H}{\partial \eta}=0 \ \ \ \text{along}\ \ \ \partial \Sigma. \end{align*}$$

It follows immediately from the above that our main theorem directly extends to critical points of ${\mathcal T}$ in this situation.

Assume that $f\colon D\to {\mathbb R}^3$ is a conformally immersed disk that is critical in ${\mathcal M}$ . We have shown that reflection at ${\mathbb R}^2$ extends the surface to a Willmore immersion $f:\widehat {{\mathbb C}} \to {\mathbb R}^3$ . Bryant proved that there exists a round sphere, such that under the associated inversion one obtains a complete minimal immersion of finite total curvature, with a finite number of flat ends [3]. In fact, Bryant’s theory includes the case of branched immersions under various assumptions; see [10, 11]. We claim that the center of a sphere with these properties is unique. Otherwise, by scaling and rotating, we can assume that $f_{\pm }: = I_{\pm } \circ f$ are minimal surfaces of that type, where $I_{\pm }$ are the inversions at the spheres of radius $\sqrt {2}$ around $\pm e_3$ . It follows that $f_{+} = I \circ f_{-}$ where $I:= I_{+} \circ I_{-}$ is the inversion $I(x) = \frac {x}{|x|^2}$ . Now in general we have the relation (see [2, (2.27)])

$$\begin{align*}\frac{1}{4} |\boldsymbol{\overrightarrow{H}}_{+}|^2\,d\mu_{+} = \frac{1}{4} |\boldsymbol{\overrightarrow{H}}_{-}|^2\,d\mu_{-} + \big(\Delta_{g_{-}} \log |f_{-}|^2\big)\,d\mu_{-}. \end{align*}$$

But in our case, $H_{+} = H_{-} = 0$ , and hence we get, away from finitely many points,

$$\begin{align*}0 = \Delta_{g_{-}}\,\log |f_{-}|^2 = \frac{4 |f_{-}^\perp|^2}{|f_{-}|^4}. \end{align*}$$

It follows that $f_{-}^\perp $ vanishes, which means that $f_{\pm }$ are conical about the origin. But there is no smooth minimal cone in ${\mathbb R}^3$ except the plane. Thus, unless our initial surface is a round half-sphere, the center of inversion lies on ${\mathbb R}^2$ and f is an inverted minimal surface with ${\mathbb R}^2$ symmetry.

In Bryant’s list, the first example is the Morin surface, which is symmetric even under a rotation by $\frac {\pi }{2}$ . It is the inversion of (see e.g., [6])

$$\begin{align*}f\colon {\mathbb C}^2\backslash \{p_1,\dots,p_4\} \longrightarrow {\mathbb R}^3, \, f(w)=\Re \left( \frac{i(w^3-w),(w^3+w),\frac{i}{2}(w^4+1)}{w^4+2\sqrt{3}w^2-1} \right), \end{align*}$$

where the $p_i$ , $1\le i\le 4$ , are the zeros of the function in the denominator of this expression. It is easy to see that the image of f contains the y-axis, and hence the Morin surface is invariant under reflections at this line, and thus we have found an example for the case in which we confine the immersion to a given support line. Additionally, it follows that the conjugate surface $f^\star $ is invariant under reflections at the $xz$ -plane. This inversion of $f^\star $ thus yields an example for the other situation considered in this paper.

Another example for the reflection at a plane is obtained from the catenoid with conformal parametrization

$$\begin{align*}f(s,\theta) = 2\,(\cosh s \cos \theta,\cosh s \sin \theta, s) \quad \mbox{ for }s,\theta \in {\mathbb R}. \end{align*}$$

Inverting the catenoid yields a bounded surface that has a double point at the origin with horizontal tangent plane, corresponding to $s \to \pm \infty $ . Substituting $s+i \theta = \log w,$ where $w = \varrho e^{i\theta }$ , we obtain for the induced metric

$$\begin{align*}g_{ij} = \frac{1+2\varrho^2 + \varrho^4} {(1+ 2\varrho^2 + \varrho^4 + 4\varrho^2 \log^2 \varrho)^2}\,\delta_{ij} = \big(1-4\varrho^2 \log^2 \varrho + {\mathcal O}(\varrho^2)\big)\,\delta_{ij} \end{align*}$$

as $\varrho \to 0$ . This parametrization is $W^{2,2}$ -conformally immersed near $w = 0$ . Now restricting to $-\frac {\pi }{2} \leq \theta \leq \frac {\pi }{2}$ gives a surface that meets the vertical plane $x_1 = 0$ orthogonally. Moreover, for $\theta = \pm \frac {\pi }{2}$ , the free boundary condition (1.6) holds; namely, we have $\partial _\eta H = 0$ by rotational symmetry. But for this we have to exclude the origin, in fact the mean curvature vector has a singular expansion [9]

$$\begin{align*}\boldsymbol{\overrightarrow{H}} = - (\log \varrho)\,e_3 + \mathcal{O}(1) \quad \mbox{ as } \varrho \to 0. \end{align*}$$

If the first variation would vanish for all admissible vector fields, then we could apply our main theorem to conclude that reflection at the plane $x_1=0$ produces a smooth extension. Thus, the example only matches our assumptions away from the two singular points. Therefore, the regularity result does not follow if the boundary condition is only satisfied away from a point.

2 Reflection at a Plane

Let us start by recalling that for $u \in W^{1,2}(Q_{\pm }),$ we have the upper and lower traces $u_{\pm } \in L^2(I)$ . We note that $u_{-} = \pm u_{+}$ for u even (resp. odd).

Lemma 2.1 The following holds for any $u \in W^{1,2}(Q_{\pm })$ .

1. (i) $\partial _x u$ is the weak derivative on Q.

2. (ii) $\partial _y u$ is the weak derivative on Q if and only if $u_{\pm }$ coincide.

Proof We have $u(\cdot,y) \in W^{1,2}(I)$ for almost every $y \in (-1,1)$ . For statement (i) we compute for $\varphi \in C^\infty _c(Q)$ using Fubini:

$$ \begin{align*} \int_Q u \partial_x \varphi\,dxdy & = \int_{-1}^1 \Big(\int_{-\pi}^{\pi} u(x,y) \partial_x \varphi(x,y)\,dx\Big)\,dy\\ & = - \int_{-1}^1 \Big(\int_{-\pi}^{\pi} \partial_x u(x,y) \varphi(x,y)\,dx\Big)\,dy\\ & = \int_Q (\partial_x u) \varphi\,dxdy. \end{align*} $$

For statement (ii), we use

$$ \begin{align*} \int_Q u \partial_y \varphi & = \int_{Q_{+}} u \partial_y \varphi + \int_{Q_{-}} u \partial_y \varphi\\ & = -\int_I u_{+} \varphi\,dx - \int_{Q_{+}} (\partial_y u) \varphi + \int_I u_{-} \varphi \,dx - \int_{Q_{-}} (\partial_y u) \varphi\\ & = \int_I (u_{-}-u_{+}) \varphi\,dx - \int_Q (\partial_y u) \varphi.\end{align*} $$

▪

By the Sobolev embedding theorem, a function $u \in W^{2,2}(Q_{\pm })$ has a representative in $C^{0,\alpha }(\overline {Q}_{\pm })$ , for any $\alpha \in [0,1)$ . In particular, the traces are given by continuous extension. Furthermore the derivatives have traces $(\partial _i u)_{\pm } \in L^2(I)$ . In the following, we need the concept of $W^{2,2}$ conformal immersions; see [7].

Lemma 2.2 Let $f:Q_{+} \to {\mathbb R}^3$ be a $W^{2,2}$ conformal immersion meeting the horizontal plane ${\mathbb R}^2$ orthogonally along I; that is,

(2.1) $$ \begin{align} f_3 & = 0 \quad \mbox{ on }I, \end{align} $$

(2.2) $$ \begin{align} \langle \nu_{+}, e_3 \rangle & = 0 \quad \mbox{ a.e. on } I\quad \mbox{ where } \nu = \frac{\partial_x f \times \partial_y f}{|\partial_x f \times \partial_y f|}. \end{align} $$

Let f be extended to Q by reflection at ${\mathbb R}^2$ , that is

(2.3) $$ \begin{align} f_i(x,y) = f_i(x,-y) \,\mbox{ for } i = 1,2, \quad f_3(x,y) = - f_3(x,-y). \end{align} $$

Then $f\colon Q \to {\mathbb R}^3$ is a $W^{2,2}$ conformal immersion.

Proof We first note that $\partial _x f \times \partial _y f \in W^{1,2} \cap L^\infty (Q_{+},{\mathbb R}^3)$ and

$$\begin{align*}{\mathrm{ess\,inf\,}} |\partial_x f \times \partial_y f| \geq e^{2\lambda}> 0 \quad \mbox{ for some }\lambda \in {\mathbb R}. \end{align*}$$

The Sobolev chain rule yields that $\nu \in W^{1,2}(Q_{+},{\mathbb R}^3)$ so that the trace $\nu _{+} \in L^\infty (I)$ is defined. The functions $f_i$ , $i = 1,2$ , are even, while $f_3$ is odd and vanishes on I by assumption (2.1). Thus, Lemma 2.1 yields directly $f \in W^{1,2}(Q,{\mathbb R}^3)$ . To see that f is actually of class $W^{2,2}(Q,{\mathbb R}^3),$ we show that

(2.4) $$ \begin{align} (\partial_x f_3)_{+} & = 0 &&\mbox{ on }I, \end{align} $$

(2.5) $$ \begin{align} (\partial_y f_i)_{+} & = 0 &&\mbox{ on }I \quad \mbox{ for } i = 1,2. \end{align} $$

These are the odd derivatives; the others are even. For given $\varphi \in C^\infty _c(Q_{+} \cup I),$ we calculate using the divergence theorem and partial integration with respect to $\partial _x$ :

$$ \begin{align*} \int_I (\partial_x f_3)_{+} \varphi\,dx & = - \int_{Q_{+}} \partial_y (\partial_x f_3)\, \varphi\,dxdy - \int_{Q_{+}} (\partial_ x f_3)\, \partial_y \varphi\,dxdy\\ & = - \int_{Q_{+}} \partial_x (\partial_y f_3)\, \varphi\,dxdy + \int_{Q_{+}} f_3\, \partial_x (\partial_y \varphi)\,dxdy\\ & = \int_{Q_{+}} (\partial_y f_3)\, \partial_x \varphi\,dxdy + \int_{Q_{+}} f_3\, \partial_y (\partial_x \varphi)\,dxdy\\ & = - \int_I f_3\, \partial_x \varphi\,dx\\ & = 0. \end{align*} $$

Since $\varphi $ is arbitrary, we get (2.4); more precisely, we have shown that

$$\begin{align*}(\partial_x f_3)_{+} = \partial_x (\,f_3|_I) = 0. \end{align*}$$

Next we claim that almost everywhere on $I,$ we have the equations

(2.6) $$ \begin{align} \big|(\partial_x f)_{+}|^2 - \big|(\partial_y f)_{+}|^2 & = \big\langle (\partial_x f)_{+},(\partial_y f)_{+} \big\rangle = 0, \end{align} $$

(2.7) $$ \begin{align} \big|(\partial_x f)_{+} \times (\partial_y f)_{+}\big| & \geq e^{2\lambda}. \end{align} $$

To see this, we use that for any $u \in W^{1,2}(Q_{+}),$ there exists a sequence $y_k \searrow 0$ such that

$$\begin{align*}u(\cdot,y_k) \to u_{+} \quad \mbox{ almost everywhere and in }L^2(I). \end{align*}$$

More precisely, there is a null set $N \subset (0,1)$ such that any sequence $y_k \searrow 0$ with $y_k \notin N$ has a subsequence with this property. Therefore, we can chose $y_k \searrow 0$ with

$$\begin{align*}\partial_x f(\cdot,y_k) \to (\partial_x f)_{+},\quad \partial_y f(\cdot,y_k) \to (\partial_y f)_{+},\quad \nu(\cdot,y_k) \to \nu_{+}. \end{align*}$$

We can further assume that almost everywhere on I

$$ \begin{align*} |\partial_x f(\cdot,y_k)|^2 - |\partial_y f(\cdot,y_k)|^2& = \langle \partial_x f(\cdot,y_k), \partial_y f(\cdot,y_k) \rangle =0, \\ |\partial_x f(\cdot,y_k) \times \partial_y f(\cdot,y_k)| &\geq e^{2\lambda}. \end{align*} $$

Passing to limits proves (2.6) and (2.7). We now verify (2.5) for a.e. $(x,0) \in I$ . We can assume $(\partial _y f)_{+}(x,0) \neq 0$ ; hence, (2.6) and (2.4) imply $(\partial _x f)_{+}(x,0) \in {\mathbb R}^2 \backslash \{0\}$ . Now

$$\begin{align*}\nu_{+} = \frac{(\partial_x f)_{+} \times (\partial_y f)_{+}}{|(\partial_x f)_{+} \times (\partial_y f)_{+}|} \quad \mbox{ almost everywhere on }I. \end{align*}$$

By (2.2), we get that $(\partial _y f)_{+}(x,0)$ is a linear combination of $(\partial _x f)_{+}(x,0)$ and $e_3$ . But then by (2.6) the vector $(\partial _y f)_{+}(x,0)$ is a multiple of $e_3,$ which proves (2.5). Lemma 2.1 implies that the extension is of class $W^{2,2}(Q,{\mathbb R}^3)$ . Noting that the $g_{ij}$ are even functions, we conclude that f is a $W^{2,2}$ conformal immersion on Q as defined in [7].▪

The next lemma states the linearized version of the constraints (2.1), (2.2) on the boundary. Here, $\eta $ denotes the inner (upward) normal of $Q_{+}$ along I with respect to g:

(2.8) $$ \begin{align} \eta = \frac{1}{\sqrt{g_{11} \det g}} \big(g_{11} e_2 - g_{12}e_1\big). \end{align} $$

Lemma 2.3 Let $f:(-\delta,\delta ) \to W^{2,2}_{\mathrm {imm}}(Q_{+},{\mathbb R}^3)$ , $t \mapsto f(t)$ , be a curve with derivative $\frac {d}{dt}f|_{t=0} = \phi $ . If $f(t) \in {\mathcal M}$ for all $t \in (-\delta,\delta )$ , i.e., (2.1) and (2.2) hold, then

(2.9) $$ \begin{align} \langle \phi, e_3 \rangle & = 0 \quad \mbox{ along }I, \end{align} $$

(2.10) $$ \begin{align} \langle \partial_\eta \phi,\nu \rangle & = 0 \quad \mbox{ along }I. \end{align} $$

We say that $\phi \in W^{2,2} \cap W^{1,\infty }(Q_{+},{\mathbb R}^3)$ is admissible at f if it satisfies (2.9) and (2.10).

Proof Equation (2.9) is obvious. At $t=0$ the we have the following derivatives:

$$ \begin{align*} &g_{\alpha \beta}\colon(-\delta,\delta) \to W^{1,2} \cap L^\infty(Q_{+}), && \displaystyle{\frac{d}{dt}}g_{\alpha \beta}|_{t=0} = \langle \partial_\alpha \phi,\partial_\beta f \rangle + \langle \partial_\alpha f,\partial_\beta \phi \rangle,\\ &\nu:(-\delta,\delta) \to W^{1,2} \cap L^\infty(Q_{+},{\mathbb R}^3), && \displaystyle{\frac{d}{dt}}\nu|_{t=0} = - g^{\alpha \beta} \langle \nu,\partial_\alpha \phi \rangle \partial_\beta f,\\ &\eta\colon (-\delta,\delta) \to L^\infty(I,{\mathbb R}^2), && \displaystyle{\frac{d}{dt}}\eta|_{t=0} = - \big(\langle \partial_\eta \phi,\partial_\tau f \rangle + \langle \partial_\tau \phi,\partial_\eta f \rangle\big)\,\tau\\ & &&\quad - \langle \partial_\eta \phi,\partial_\eta f \rangle\,\eta. \end{align*} $$

Here, $\tau = e_1/\sqrt {g_{11}}$ is the unit tangent of I with respect to g. As g is the metric induced by f, the vector $df \cdot \eta $ is by definition orthogonal to $df \cdot e_1$ and also to $\nu $ . But these two vectors span ${\mathbb R}^2$ by (2.1) and (2.2); thus, $df \cdot \eta = \pm e_3$ . We now compute at $t = 0$ along I

$$ \begin{align*} 0 & = \frac{d}{dt} \langle \nu,e_3 \rangle|_{t=0} && \mbox{ (using } \nu \perp e_3 \mbox{ by ({2.2}))}\\ & = \pm \langle \frac{d}{dt}\nu|_{t=0},df \cdot \eta \rangle &&\mbox{ (using } df \cdot \eta = \pm e_3, \mbox{ see above)}\\ & = \mp \langle \nu,\frac{d}{dt}(df \cdot \eta)|_{t=0} \rangle && \mbox{ (using } \nu \perp df \cdot \eta\mbox{)}\\ & = \mp \langle \nu, d\phi \cdot \eta \rangle &&\mbox{ (using } \nu \perp df \cdot \frac{d}{dt}\eta|_{t=0}\mbox{)}. \end{align*} $$

In this calculation we actually used the traces of the functions $g_{ij}$ , $\nu $ , $\partial _i f$ and $\partial _i \phi $ . The trace operator is continuous from $W^{1,2} \cap L^\infty (Q_{+})$ to $L^\infty (I)$ , and therefore interchanges with the time derivative at $t = 0$ . This justifies our computation.▪

Next recall the first variation formula for the Willmore energy; see [14]. The Willmore functional ${\mathcal W}(\,f)$ is Fréchet differentiable on $W^{2,2}_{\mathrm {imm}}(Q_{+},{\mathbb R}^3)$ , with derivative

(2.11) $$ \begin{align} D{\mathcal W}(\,f)\phi &= \frac{1}{2} \int_{Q_{+}} \langle \boldsymbol{\overrightarrow{H}},\Delta_g \phi \rangle\,d\mu_g\nonumber \nonumber \\ & \quad - \int_{Q_{+}} g^{ij}g^{kl} \langle \boldsymbol{\overrightarrow{H}},A_{ik} \rangle \langle \partial_j f,\partial_k \phi \rangle\,d\mu_g \nonumber \\ &\quad+ \frac{1}{4} \int_{Q_{+}} |\boldsymbol{\overrightarrow{H}}|^2 g^{ij} \langle \partial_i f,\partial_j \phi \rangle\,d\mu_g. \end{align} $$

Theorem 2.4 Let $f \in W^{2,2}_{\mathrm {conf}}(Q_{+},{\mathbb R}^3)$ satisfy (2.1), (2.2) along I. Assume that f is Willmore critical under these constraints; i.e., whenever $\phi \in W^{2,2}\cap W^{1,\infty }(Q_{+},{\mathbb R}^3)$ is admissible at f with compact support in $Q_{+} \cup I$ , then

(2.12) $$ \begin{align} D{\mathcal W}(\,f)\phi = 0. \end{align} $$

Then extending f by reflection at ${\mathbb R}^2$ yields a smooth Willmore immersion $f\colon Q \to {\mathbb R}^3$ .

Proof We establish the weak version of the Willmore equation on all of Q. Let $R = \mathrm {diag}(1,1,-1)$ . We say that $\phi :Q \to {\mathbb R}^3$ is even (resp. odd) if and only if $\phi (x,y) = \pm R \phi (x,-y)$ . By definition, the immersion f and its derivatives $\partial _1 f,\partial _1^2 f,\partial _2^2 f$ are even, while $\partial _2 f,\partial ^2_{12} f$ are odd. The derivative $\partial _1$ preserves the parity, while $\partial _2$ changes it. One checks that the integrand in the first variation formula is odd in the case when $\phi $ is odd, so that the integral vanishes trivially in this case. For $\phi $ even, the integrand is even and

$$\begin{align*}D{\mathcal W}(\,f)\phi = 2\, D{\mathcal W}(\,f|Q_{+})\phi|_{Q_{+}}. \end{align*}$$

As $\phi $ is even, we have $\phi _3(x,0) = 0$ and $\partial _y \phi _i(x,0) = 0$ for $i = 1,2$ . Since $f|_{Q_{+}}$ is conformally parametrized, this implies $\partial _\eta \phi _i (x,0) = 0$ . Thus, the variation $\phi $ is admissible, and by assumption,

$$\begin{align*}D{\mathcal W}(\,f|Q_{+})\phi|_{Q_{+}} = 0. \end{align*}$$

It follows that the $W^{2,2}$ conformal immersion $f\colon Q \to {\mathbb R}^3$ is a critical point of the Willmore functional with respect to all compactly supported variations. The regularity theorem of Rivière [14] implies that f is a smooth Willmore immersion.▪

3 Nondegeneracy of the Boundary Condition

Here, we address the question whether any admissible $\phi $ is the tangent vector of some curve $f(t)$ of $W^{2,2}$ immersions satisfying the boundary constraints. For this, we let $f \in W^{2,2}_{\mathrm {imm}}(Q_{+},{\mathbb R}^3)$ be a given conformal immersion satisfying

(3.1) $$ \begin{align} {\mathcal B}(\,f) = \big(\langle f,e_3 \rangle,\langle \nu_f,e_3 \rangle\big) = 0 \quad \mbox{ along }I. \end{align} $$

Formally linearizing ${\mathcal B}$ at f yields the operator

(3.2) $$ \begin{align} L_f \phi = \big(\langle \phi,e_3 \rangle,\langle D\phi \cdot \eta, \nu \rangle\big). \end{align} $$

For f conformal, i.e., $g_{ij} = e^{2u} \delta _{ij}$ , the operator $L_f$ becomes

(3.3) $$ \begin{align} L_f \phi = \big(\langle \phi,e_3 \rangle, e^{-u} \langle \partial_y \phi, \nu \rangle\big). \end{align} $$

Putting $K = [-\frac {\pi }{2},\frac {\pi }{2}],$ we consider the Banach spaces

$$ \begin{align*} X & = \{(a,b) \in W^{\frac{3}{2},2}\cap W^{1,\infty}(I) \oplus W^{\frac{1}{2},2}\cap L^\infty(I): \mathrm{spt\,}(a,b) \subset K\},\\ Y & = \{\phi \in W^{2,2} \cap W^{1,\infty}(Q_{+},{\mathbb R}^2 \oplus {\mathbb R}): \mathrm{spt\,}L_f\phi \subset K\}. \end{align*} $$

We have the linear map, using the extension $BH$ from the appendix,

(3.4) $$ \begin{align} \Phi_f\colon X \longrightarrow Y,\quad\Phi_f(a,b) = BH(0,e^u b \nu_f) \oplus BH(a,0)e_3. \end{align} $$

Note that $\nu _f\colon I \to {\mathbb R}^2$ by (3.1). Since $u \in W^{1,2} \cap L^\infty (Q_{+})$ and $\nu _f \in W^{1,2} \cap L^\infty (Q_{+},{\mathbb R}^3)$ by assumption, we can estimate

(3.5) $$ \begin{align} \|\Phi_f(a,b)\|_Y \leq C\,\|(a,b)\|_X. \end{align} $$

The constant depends on the bound for f in $W^{2,2} \cap W^{1,\infty }(Q_{+},{\mathbb R}^3)$ , and on the lower bound for u, i.e., for the Jacobian of f. Now $L_f$ is a continuous operator

$$ \begin{align*} L_f\colon Y \to X,\, L_f(\phi) = \big(\langle \phi,e_3 \rangle, e^{-u} \langle \partial_y \phi,\nu \rangle\big). \end{align*} $$

Clearly, $\phi \in \mathrm {ker\,}L_f$ if and only if $\langle \phi, e_3 \rangle = 0$ , $\langle \partial _y \phi,\nu \rangle = 0$ , along I. By construction,

$$\begin{align*}L_f \circ \Phi_f = \mathrm{id}, \quad \mbox{ in particular, } \mathrm{ker\,}L_f \cap \mathrm{im\,}\Phi_f = \{0\}. \end{align*}$$

The subspace $\mathrm {im\,}\Phi _f \subset Y$ is closed: let $\phi _k = \Phi _f(a_k,b_k) \to \phi $ in Y. Then $(a_k,b_k) = L_f \phi _k \to L_f \phi =: (a,b)$ in X, which yields $\phi = \lim _{k \to \infty } \Phi _f(a_k,b_k) = \Phi _f(a,b)$ . It follows that restricting $L_f$ gives the isomorphism

$$\begin{align*}L_f|_{\mathrm{im\,}\Phi_f}:\mathrm{im\,}\Phi_f \to X, \end{align*}$$

with inverse bounded by (3.5). Moreover, we have the direct sum decomposition

$$\begin{align*}Y = \mathrm{im\,}\Phi_f \oplus \mathrm{ker\,}L_f, \quad \phi = \Phi_f (L_f \phi) \oplus \big(\phi - \Phi_f (L_f \phi)\big). \end{align*}$$

By the implicit function theorem, there exist open neighborhoods $U \subset \mathrm {ker\,}L_f$ and $V \subset \mathrm {im\,}\Phi _f$ of the origin, and a $C^1$ mapping $G\colon U \to V$ with $G(0) = 0$ , such that for $\phi \oplus \psi \in U \oplus V$ the following equivalence holds:

$$\begin{align*}f + \phi + \psi\, \mbox{ satisfies (3.1)} \quad \Longleftrightarrow \quad \psi = G[\phi]. \end{align*}$$

Here, we use that $W^{2,2}_{\mathrm {imm}}(Q_{+},{\mathbb R}^3)$ is an open subset of $W^{2,2} \cap W^{1,\infty }(Q_{+},{\mathbb R}^3)$ ; whence, for $U,V$ sufficiently small the map $f+\phi + \psi $ is weakly immersed. For any $\phi \in \mathrm {ker\,}L_f,$ we thus obtain the admissible curve of weak immersions

$$\begin{align*}f(t) = f + t \phi + G[t\phi],\quad t \in (-\delta,\delta). \end{align*}$$

We have $DG[0] = 0$ from the general construction. To see this explicitely, we note that $DG[0]\phi \in \mathrm {im\,}\Phi _f$ by definition, while differentiating at $t = 0$ shows $DG[0]\phi \in \mathrm {ker\,}L_f$ :

$$\begin{align*}0 = \frac{d}{dt}{\mathcal B}(\,f(t))|_{t=0} = L_f (\phi + DG[0]\phi) = L_f DG[0]\phi. \end{align*}$$

4 Reflection in a line

The condition of prescribing a line for the boundary with free tangent plane is similar and in fact simpler than the previous one. We indicate the main points.

Lemma 4.1 Let $f:Q_{+} \to {\mathbb R}^3$ be a $W^{2,2}$ conformal immersion, that is

(4.1) $$ \begin{align} \!\!\!\!\!|\partial_x f \times \partial_y f| & \geq \mu> 0 && \!\mbox{ in }Q_{+}, \end{align} $$

(4.2) $$ \begin{align} \!\!\langle \partial_x f,\partial_y f \rangle & = 0 && \,\,\;\;\;\;\;\; \mbox{ in }Q_{+}, \end{align} $$

(4.3) $$ \begin{align} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! |\partial_x f|^2 - |\partial_y f|^2 & = 0 && \,\,\,\;\;\;\;\; \mbox{ in }Q_{+}. \end{align} $$

Assume that $f|_I$ maps into the line $L = \{0\} \times {\mathbb R} \subset {\mathbb R}^3$ ; i.e.,

(4.4) $$ \begin{align} f_i = 0 \quad \mbox{ along } I \mbox{ for }i = 1,2. \end{align} $$

Let f be extended to all of Q by reflection at L, that is

(4.5) $$ \begin{align} f_i(x,y) & = -f_i(x,-y) \quad \mbox{ for } i = 1,2, \end{align} $$

(4.6) $$ \begin{align} f_3(x,y) & = f_3(x,-y). \end{align} $$

Then $f\colon Q \to {\mathbb R}^3$ is a $W^{2,2}$ conformal immersion.

Proof The function $f_3$ is even, while $f_i$ , $i =1,2$ , are odd with $f_i(x,0) = 0$ by assumption (4.4). Thus $f \in W^{1,2}(Q,{\mathbb R}^3)$ by Lemma 2.1. To see that $f \in W^{2,2}(Q,{\mathbb R}^3)$ we need to show the vanishing of the odd first derivatives, i.e.,

$$\begin{align*}\partial_x f_i = 0 \mbox{ on }I \mbox{ for } i=1,2 \quad \mbox{ and } \quad \partial_y f_3 = 0 \mbox{ on } I. \end{align*}$$

The first follows by differentiating the equation $f_i(x,0) = 0$ (copy the argument for $f_3$ from Lemma 2.2). To show the second statement at a point $(x,0)$ , we can assume $\partial _y f(x,0) \neq 0$ . Then $\partial _x f(x,0)$ is also nonzero. But $\partial _x f(x,0)$ is a multiple of $e_3$ . By conformality, $\partial _y f(x,0)$ then lies in ${\mathbb R}^2$ , i.e., $\partial _y f_3(x,0) = 0$ .▪

Theorem 4.2 Let $f:Q_{+} \to {\mathbb R}^3$ be a $W^{2,2}$ conformal immersion with $f_i = 0$ for $i = 1,2$ along I. Assume that f is critical under these constraints, i.e.,

(4.7) $$ \begin{align} D{\mathcal W}(\,f)\phi = 0 \quad \mbox{ for all admissible } \phi \in W^{2,2} \cap W^{1,\infty}(Q_{+},{\mathbb R}^3), \end{align} $$

that is, $\phi $ has compact support in $Q_{+} \cup I$ and $\phi _i|_I = 0$ for $i = 1,2$ . Then extending f by reflection at $L = \{0\} \times {\mathbb R}$ yields a smooth Willmore immersion $f\colon Q \to {\mathbb R}^3$ .

Proof We establish the weak version of the Willmore equation on all of Q. Let $S = \mathrm {diag}(-1,-1,1)$ . We say that $\phi :Q \to {\mathbb R}^3$ is even (resp. odd) if and only if $\phi (x,y) = \pm S \phi (x,-y)$ . By definition, the immersion f and its derivatives $\partial _1 f, \partial ^2_{11} f, \partial ^2_{22} f$ are even, while $\partial _2 f,\partial _{12} f$ are odd. The derivative $\partial _1$ preserves the parity, while $\partial _2$ changes it. One checks (!) that the integrand in the first variation formula is odd in the case when $\phi $ is odd, so that the integral vanishes trivially in this case. For $\phi $ even the integrand is even, and one obtains

$$\begin{align*}D{\mathcal W}(\,f)\phi = 2\, D{\mathcal W}(\,f|Q_{+})\phi|_{Q_{+}}. \end{align*}$$

Now $\phi $ even implies $\phi _i(x,0) = 0$ for $i = 1,2$ , and hence the variation $\phi $ is admissible on $Q_{+}$ , so that by assumption

$$\begin{align*}D{\mathcal W}(\,f|Q_{+})\phi|_{Q_{+}} = 0. \end{align*}$$

It follows that the $W^{2,2}$ conformal immersion $\phi :Q \to {\mathbb R}^3$ is a critical point of the Willmore functional. The regularity theorem of Rivière [14] implies that f is a smooth Willmore immersion.▪

In contrast to Section 3, here both boundary constraints are linear; hence, the affine variation suffices to generate any given admissible field $\phi $ .

5 Critical points of related curvature energies

In this section, we discuss the same subject for the two related functionals

(5.1) $$ \begin{align} {\mathcal E}(\,f) & = \frac{1}{2} \int_{\Sigma} |h|^2\,d\mu_g, \end{align} $$

(5.2) $$ \begin{align} {\mathcal T}(\,f) & = \frac{1}{2} \int_{\Sigma} |h^\circ|^2\,d\mu_g. \end{align} $$

As is well known, the integrand of the Thomsen functional ${\mathcal T}(\,f)$ is pointwise conformally invariant [17]. Clearly, $|h|^2 = |h^\circ |^2 + \frac {1}{2}H^2$ ; hence,

(5.3) $$ \begin{align} {\mathcal E}(\,f) = {\mathcal T}(\,f) + {\mathcal W}(\,f). \end{align} $$

Assuming enough regularity, we can rewrite the functionals using Gauß-Bonnet, i.e.,

(5.4) $$ \begin{align} {\mathcal{E}}(\,f) = 2\, {\mathcal{W}}(\,f) + \int_{\partial \Sigma} \kappa_g\,ds - 2\pi \chi(\Sigma), \end{align} $$

(5.5) $$ \begin{align} {\mathcal T}(\,f) & = {\mathcal W}(\,f) + \int_{\partial \Sigma} \kappa_g\,ds - 2\pi \chi(\Sigma). \end{align} $$

Therefore, both functionals have $W(\,f)$ as Euler–Lagrange operator, with factor $\frac {1}{2}$ for ${\mathcal T}(\,f)$ . Let $N^S$ be the interior unit normal along $S = \partial \Omega $ , and let $\eta $ be the interior unit normal along $\partial \Sigma $ with respect to the induced metric g. As before, we denote by ${\widetilde {\mathcal M}}(S)$ the class of smooth immersions $f\colon \Sigma \to {\mathbb R}^3$ satisfying the constraints

(5.6) $$ \begin{align} f(\partial \Sigma) \subset S \quad \mbox{ and } \quad \frac{\partial f}{\partial \eta} = N^S \circ f. \end{align} $$

Differentiating in the direction of the unit tangent $\tau = \frac {\partial }{\partial s}$ along $\partial \Sigma,$ we obtain, using also $\langle \nu, N^S \circ f \rangle = 0$ ,

$$\begin{align*}0 = \partial_s \langle \partial_s f, N^S \circ f \rangle = \big \langle Df \cdot \nabla_\tau \tau, N^S \circ f \big\rangle + \big\langle \partial_s f, (DN^S) \cdot \partial_s f \big\rangle. \end{align*}$$

Now by definition $\nabla _\tau \tau = \kappa _g \eta $ . Using (5.6) again, we see that

(5.7) $$ \begin{align} \kappa_g = h^S \big(\partial_s f, \partial_s f\big). \end{align} $$

We conclude that for $f \in {\widetilde {\mathcal M}}(S),$ we have

(5.8) $$ \begin{align} {\mathcal E}(\,f) & = 2\, {\mathcal W}(\,f) + \int_{\partial \Sigma} h^S \big(\partial_s f, \partial_s f\big)\,ds - 2\pi \chi(\Sigma), \end{align} $$

(5.9) $$ \begin{align} {\mathcal T}(\,f) & = {\mathcal W}(\,f) + \int_{\partial \Sigma} h^S \big(\partial_s f, \partial_s f\big)\,ds - 2\pi \chi(\Sigma). \end{align} $$

On ${\widetilde {\mathcal M}}({\mathbb R}^2)$ the three functionals $\mathcal {E}$ , $\mathcal {T}$ , and $\mathcal {W}$ coincide up to a topological constant, in particular they have the same critical points. Next we compute the resulting free boundary conditions.

Lemma 5.1 For a smooth variation $f(\cdot,t):\Sigma \to {\mathbb R}^3$ , $t \in (-\delta,\delta )$ with velocity $\phi = \varphi \nu + Df \cdot \xi,$ we have

(5.10) $$ \begin{align} \frac{d}{dt} {\mathcal E}(\,f(\cdot,t))|_{t=0} &= \int_{\Sigma} {W}(\,f) \varphi \, d\mu_g +\int_{\partial \Sigma} \tau (\eta)\,ds_g, \quad \mbox{ where } \end{align} $$

(5.11) $$ \begin{align} \tau(\eta) &= \frac{\partial H}{\partial \eta} \varphi - h(\mathrm{grad}_g \varphi,\eta) - \frac{1}{2} |h|^2 g(\xi,\eta). \end{align} $$

Proof Assume first that $\phi $ is normal. The following identities in general codimension are computed in [8]:

$$ \begin{align*} \partial_t g_{\alpha \beta} & = - 2 h_{\alpha \beta}\varphi,\\ \partial_t (d\mu_g) & = - H\varphi \, d\mu_g,\\ \partial_t h_{\alpha \beta} & = \nabla^2_{\alpha \beta}\varphi - g^{\lambda \mu} h_{\alpha \lambda} h_{\beta \mu} \varphi . \end{align*} $$

We compute further, using normal coordinates at $t= 0$ , $p \in \Sigma $ ,

$$ \begin{align*} \partial_t \Big(\frac{1}{2} |h|^2 d\mu_g\Big) & = \frac12 \partial_t \big(g^{\alpha \lambda}g^{\beta \mu} h_{\alpha \beta}h_{\lambda \mu} \,d\mu_g\big)\\ & = \big( \nabla^2_{\alpha \beta} \varphi - h_{\alpha \gamma} h_{\beta \gamma} \varphi \big)h_{\alpha \beta} \,d\mu_g - \frac{1}{2} |h|^2\, H\varphi\,d\mu_g\\ &\quad +2\, h_{\alpha \lambda} h_{\alpha \beta}h_{\lambda \beta} \varphi \,d\mu_g. \end{align*} $$

Decomposing $h_{\alpha \beta } = h^\circ _{\alpha \beta } + \frac {1}{2} H \delta _{\alpha \beta }$ yields

(5.12) $$ \begin{align} h_{\alpha \lambda} h_{\alpha \beta}h_{\lambda \beta} = \frac32 |h^\circ|^2 H+\frac14 H^2H. \end{align} $$

We finally arrive at

(5.13) $$ \begin{align} \partial_t \Big(\frac{1}{2} |h|^2 d\mu_g\Big) = \big(h \nabla^2 \varphi + |h^\circ|^2H\varphi \big)\,d\mu_g. \end{align} $$

Now we compute, still in normal coordinates, using that $\nabla _i h_{ik} = \nabla _k H$ by Codazzi,

$$ \begin{align*} h\nabla^2 \varphi - \varphi \Delta H & = \frac{1}{\sqrt{\det g}} \partial_\alpha \big(\sqrt{\det g}\, g^{\alpha \beta} \tau_\beta \big), \quad \mbox{ where }\\ \tau_\beta & = g^{\lambda \mu} \nabla_\lambda \varphi h_{\beta \mu} - \varphi \nabla_\beta H . \end{align*} $$

Next, consider a tangential variation of the form $f \circ \varphi _t$ , where $\varphi _t$ is the flow of a vectorfield $\xi $ . Then we have

$$\begin{align*}{\mathcal E}(\,f \circ \varphi_t,\Omega) = {\mathcal E}(\,f,\varphi_t(\Omega))\\ = \frac{1}{2} \int_\Omega |h|^2(\varphi_t(x)) J_g\varphi_t(x)\,d\mu_g(x). \end{align*}$$

Differentiating at $t = 0,$ we obtain

$$\begin{align*}\frac{d}{dt}{\mathcal E}(\,f \circ \varphi_t,\Omega)|_{t=0} = \frac{1}{2} \int_{\Omega} \big(d|h|^2(\xi) + |h|^2 \mathrm{div_g}\xi\big)\,d\mu_g = \frac{1}{2} \int_{\Omega} \mathrm{div_g} (|h|^2 \xi)\,d\mu_g. \end{align*}$$

Now $g(|h|^2 \xi,X) = |h|^2 \langle \phi, df \cdot X \rangle $ . The claim of the lemma follows by combining the two computations.▪

Now assume that f is a critical point in ${\mathcal M}(S)$ . As computed in [1], a variation $\phi = \varphi \nu + Df \cdot \xi $ is admissible if and only if

(5.14) $$ \begin{align} g(\xi,\eta) = 0 \quad \mbox{ and }\quad \frac{\partial \varphi}{\partial \eta} + \varphi h^S(\nu,\nu) = 0 \quad \mbox{ on } \partial \Sigma. \end{align} $$

It is easy to see that for given functions $\varphi,\mu $ on $\partial \Sigma $ , there exists an admissible variation $\phi $ such that $\phi = \varphi \nu + \mu \partial _s f$ along $\partial \Sigma $ . Now if f is critical in ${\widetilde {\mathcal M}}(S)$ , then $W(\,f) = 0$ and further for $\phi $ admissible

$$\begin{align*}0 = \int_{\partial \Sigma} \Big(\varphi \frac{\partial H}{\partial \eta} - h(\mathrm{grad}_g \varphi,\eta) -\frac{1}{2}|h|^2 g(\xi,\eta)\Big)\,ds_g. \end{align*}$$

We have $g(\xi,\eta ) = 0$ from (5.14). Furthermore,

$$ \begin{align*} h(\mathrm{grad}_g \varphi,\eta) & = (\partial_\tau \varphi) h(\tau,\eta) + (\partial_\eta \varphi) h(\eta,\eta)\\ & = \partial_\tau (\varphi h(\tau,\eta)) - \varphi \nabla_\tau h(\tau,\eta) - \varphi h(\nabla_\tau \tau,\eta) - \varphi h(\tau,\nabla_\tau \eta)\\ & = \partial_\tau (\varphi h(\tau,\eta)) - \varphi \nabla_\tau h(\tau,\eta) - \varphi \kappa_g h(\eta,\eta) + \varphi \kappa_g h(\tau,\tau). \end{align*} $$

We arrive at the formula

$$\begin{align*}0 = \int_{\partial \Sigma} \Big(\varphi \frac{\partial H}{\partial \eta} - \frac{\partial \varphi}{\partial \eta} h(\eta,\eta) + \varphi\big[\nabla_\tau h(\tau,\eta) + \kappa_g \big(h(\eta,\eta)-h(\tau,\tau)\big)\big]\Big)\,ds_g. \end{align*}$$

Now differentiating the constraint $\langle \nu,N^S \circ f \rangle =0$ in direction of $\tau $ , we get

$$ \begin{align*} 0 & = \partial_\tau \langle \nu,N^S \circ f \rangle\\ & = \langle Df \cdot W \tau, Df \cdot \eta \rangle + \langle \nu, (DN^S) \circ f Df \cdot \tau \rangle\\ & = h(\tau,\eta) + h^S(\nu,Df \cdot \tau). \end{align*} $$

Differentiating once more yields

$$\begin{align*}\nabla_\tau h(\tau,\eta) + \kappa_g \big(h(\eta,\eta)-h(\tau,\tau)\big) + \partial_s \big[h^S(\nu, \partial_s f)\big] = 0. \end{align*}$$

Inserting this into the boundary condition, we finally get

$$ \begin{align*} 0 & = \int_{\partial \Sigma} \Big(\varphi \frac{\partial H}{\partial \eta} - \frac{\partial \varphi}{\partial \eta} h(\eta,\eta) - \varphi\,\partial_s \big[h^S(\nu, \partial_s f)\big]\Big)\,ds_g\\ & = \int_{\partial \Sigma} \varphi\, \Big(\frac{\partial H}{\partial \eta} + h(\eta,\eta)h^S(\nu,\nu) - \partial_s \big[h^S(\nu, \partial_s f)\big]\Big)\,ds_g. \end{align*} $$

Thus, we obtained the boundary condition

(5.15) $$ \begin{align} \frac{\partial H}{\partial \eta} + h^S(\nu,\nu)h(\eta,\eta) - \partial_s \big[h^S(\nu, \partial_s f)\big] = 0. \end{align} $$

Clearly, this reduces to $\frac {\partial H}{\partial \eta } = 0$ when S is a plane. For a sphere $S = \partial B_R(0),$ we get

$$\begin{align*}\frac{\partial H}{\partial \eta} + \frac{1}{R} h(\eta,\eta) = 0. \end{align*}$$

To get the boundary condition for the Thomsen functional $\mathcal {T,}$ one just combines the results for ${\mathcal W}(\,f)$ and ${\mathcal E}(\,f)$ ; we just state the equations:

$$ \begin{align*} 0 & = \frac{\partial H}{\partial \eta} + h^S(\nu,\nu) H = 0,\\ 0 & = \frac{\partial H}{\partial \eta} + h^S(\nu,\nu) (h(\eta,\eta-h(\tau,\tau)) - \partial_s \big[h^S(\nu, \partial_s f)\big]. \end{align*} $$

The above computations all assumed sufficient regularity. For the application of our main theorem, we need (5.8) and (5.9) for conformal immersions that are only in $\mathcal {M}$ . This follows directly from a reflection argument using Lemma 2.2 and the Gauss–Bonnet theorem for closed surfaces from [7].

A APPENDIX Extension Lemma

Here we extend compactly supported functions on ${\mathbb R}$ to the upper halfplane with certain bounds. Such an extension was also mentioned in [16]. In addition to the previous notation, we put $K = [-\frac {\pi }{2},\frac {\pi }{2}]$ and $\mathbb {H} = {\mathbb R} \times [0,\infty )$ .

Lemma A.1 (Extension)

Let $\varphi \in W^{\frac {3}{2},2} \cap W^{1,\infty }({\mathbb R})$ , $\psi \in W^{\frac {1}{2},2} \cap L^\infty ({\mathbb R})$ have support in K. There exists $u \in W^{2,2} \cap W^{1,\infty }(\mathbb {H})$ with compact support in $I \times [0,1)$ , such that

(A.1) $$ \begin{align} u(\cdot,0) = \varphi \quad \mbox{ and } \quad \frac{\partial u}{\partial y}(\cdot,0) = \psi, \end{align} $$

and such that for a universal constant $C< \infty,$ one has the estimates

(A.2) $$ \begin{align} \|u\|_{C^1} & \leq C \,\big(\|\varphi\|_{W^{1,\infty}} + \|\psi\|_{L^\infty}\big), \end{align} $$

(A.3) $$ \begin{align} \|u\|_{W^{2,2}} & \leq C \, \big(\|\varphi\|_{W^{\frac{3}{2},2}} + \|\psi\|_{W^{\frac{1}{2},2}}\big), \end{align} $$

Proof We start by considering the harmonic extension

(A.4) $$ \begin{align} H\varphi\colon \mathbb{H} \longrightarrow {\mathbb R},\, H\varphi(x,y) = \sum_{k=0}^\infty \varphi_k(x) e^{-ky}. \end{align} $$

Here, $\varphi = \sum _{k=0}^\infty \varphi _k$ is the Fourier decomposition on I. We compute

$$ \begin{align*} H\varphi(x,y) & = \frac{1}{\pi}\sum_{k=0}^\infty \Big(\int_I \varphi(x') \cos (kx')\,dx'\Big) \cos kx\, e^{-ky}\\ &\quad + \frac{1}{\pi}\sum_{k=0}^\infty \Big(\int_I \varphi(x') \sin (kx')\,dx'\Big) \sin kx\, e^{-ky}\\ & = \frac{1}{\pi} \int_I \varphi(x') \sum_{k=0}^\infty \cos k(x-x')\, e^{-ky}\,dx'\\ & = \frac{1}{\pi}\, \mathrm{Re\,}\int_I \varphi(x') \sum_{k=0}^\infty e^{k(-y+i(x-x'))}\,dx'\\ & = \frac{1}{\pi}\, \mathrm{Re\,}\int_I \varphi(x')\frac{1}{1- e^{-y+i(x-x')}}\,dx'\\ & = \frac{1}{\pi}\, \int_I \varphi(x') \frac{1-e^{-y}\cos (x-x')}{1-2e^{-y} \cos (x-x') + e^{-2y}}\,dx'\\ & = \frac{1}{2\pi}\, \int_I \varphi(x') \frac{e^y - \cos (x-x')}{\cosh y - \cos (x-x')}\,dx'. \end{align*} $$

Thus, we have

$$\begin{align*}H\varphi(x,y) = \int_I G(x-x',y)\varphi(x')\,dx', \quad \mbox{ where }G(x,y) = \frac{1}{2\pi}\,\frac{e^y - \cos x}{\cosh y - \cos x}. \end{align*}$$

For $\varphi (x) \equiv 1,$ we have $H \varphi \equiv 1$ , which yields noting $G(-x,y) = G(x,y)$ ,

$$\begin{align*}\int_I G(x,y)\,dx = 1 \quad \mbox{ for all }y> 0. \end{align*}$$

In particular, for any $y> 0,$ we can estimate

(A.5) $$ \begin{align} \|H\varphi(\cdot,y)\|_{C^0(I)} \leq \|\varphi\|_{L^\infty(I)}. \end{align} $$

Using the Cauchy estimate on the disk $D_y((x,y))$ we get, again for $y> 0$ ,

(A.6) $$ \begin{align} \|D(H \varphi)(\cdot,y)\|_{C^0(I)} \leq \frac{C}{y} \,\|\varphi\|_{L^\infty(I)}. \end{align} $$

Now the biharmonic extension $u = BH(\varphi,\psi )$ is given by

$$\begin{align*}u(x,y) = H\varphi(x,y) - y\, \partial_y(H\varphi)(x,y) + y H\psi(x,y). \end{align*}$$

The extension has initial values

$$\begin{align*}u(x,0) = H\varphi(x,0) = \varphi(x) \quad \mbox{ and } \quad \partial_y u(x,0) = H\psi(x,0) = \psi(x). \end{align*}$$

To see that $u(x,y)$ is biharmonic, we note for $h(x,y)$ harmonic that

$$\begin{align*}\Delta (y h(x,y)) = 2\, \partial_y h(x,y); \quad \mbox{ thus, }\quad \Delta^2 (y h(x,y)) = 2 \partial_y \Delta h(x,y) = 0. \end{align*}$$

Now we collect the relevant estimates. By (A.5) and (A.6), we get, for $0 < y \leq 1,$

(A.7) $$ \begin{align} \|u(\cdot,y)\|_{C^0(I)} \leq C \|\varphi\|_{L^\infty(I)} + y \|\psi\|_{L^\infty(I)}. \end{align} $$

Writing $\partial _x u = H\varphi ' -y \,\partial _y (H\varphi ') + y \partial _x (H\psi ),$ we get by the above estimates,

(A.8) $$ \begin{align} \|\partial_x u(\cdot,y)\|_{C^0(I)} \leq C \big(\|\varphi'\|_{L^\infty(I)} + \|\psi\|_{L^\infty(I)}\big). \end{align} $$

Using that $H \varphi $ is harmonic, now we have

$$\begin{align*}\partial_y u = - y\, \partial_y^2 (H\varphi) + H\psi + y\, \partial_y(H\psi) = y\, \partial_x (H\varphi') + H\psi + y\, \partial_y(H\psi); \end{align*}$$

whence, by the above estimates,

(A.9) $$ \begin{align} \|\partial_y u(\cdot,y)\|_{C^0(I)} \leq C\, \big(\|\varphi'\|_{L^\infty(I)} + \|\psi\|_{L^\infty(I)}\big). \end{align} $$

For the $L^2$ estimates, we have for any $s \in {\mathbb R}$ by orthogonality of the $\varphi _k,$

$$ \begin{align*} \big\|\sum_{k=1}^\infty k^s \varphi_k(x) e^{-ky}\|^2_{L^2(I \times (0,\infty))} & = \sum_{k = 1}^\infty k^{2s} \|\varphi_k\|_{L^2(I)}^2\,\int_0^\infty e^{-2ky}\,dy\\ & = \frac{1}{2} \sum_{k=1}^\infty k^{2s-1} \|\varphi_k\|_{L^2(I)}^2\\ & = \frac{1}{2} \big[\varphi\big]^2_{W^{s - \frac{1}{2},2}(I)}. \end{align*} $$

Now for $i,j \in {\mathbb N}_0,$ we have $\partial _x^i \partial _y^j\, (H\varphi ) = (-1)^j \sum _{k=0}^\infty \varphi _k^{(i)}(x)\,k^je^{-ky}$ . As $\|\varphi _k^{(i)}\|_{L^2(I)} = k^i\,\|\varphi _k\|_{L^2(I)}$ , by putting $s = 0,1,2,$ we get

$$ \begin{align*} \|H(\varphi-\varphi_0)\|_{L^2(I \times (0,\infty))} & \leq C [\varphi]_{W^{-\frac{1}{2},2}(I)},\\ \|D(H \varphi)\|_{L^2(I \times (0,\infty))} & \leq C [\varphi]_{W^{\frac{1}{2},2}(I)},\\ \|D^2(H \varphi)\|_{L^2(I \times (0,\infty))} & \leq C [\varphi]_{W^{\frac{3}{2},2}(I)}. \end{align*} $$

In the following we put $\|\varphi \|^2_{W^{s,2}(I)} = |\varphi _0|^2 + [\varphi ]^2_{W^{s,2}(I)}$ . For the biharmonic extension u we deduce the following estimates:

$$ \begin{align*} \|u\|_{L^2(I \times (0,1))} & \leq C\, \big(\|\varphi\|_{W^{\frac{1}{2},2}(I)} + \|\psi\|_{W^{-\frac{1}{2},2}(I)}\big),\\ \|D u\|_{L^2(I \times (0,1))} & \leq C\, \big([\varphi]_{W^{\frac{3}{2},2}(I)} + [\psi]_{W^{\frac{1}{2},2}(I)}\big),\\ \|\Delta u\|_{L^2(I \times (0,1))} & = 2\, \|-\partial_y^2 (H\varphi) + \partial_y (H\psi)\|_{L^2(I \times (0,1))}\\ & = 2\, \|H\varphi'' + \partial_y (H\psi)\|_{L^2(I \times (0,1))}\\ & \leq C\, \big([\varphi'']_{W^{-\frac{1}{2},2}(I)} + [\psi]_{W^{\frac{1}{2},2}(I)}\big)\\ & = C\, \big([\varphi]_{W^{\frac{3}{2},2}(I)} + [\psi]_{W^{\frac{1}{2},2}(I)}\big). \\ \end{align*} $$

To estimate the full second derivatives we integrate by parts:

$$ \begin{align*} &\int_{I \times (0,1)} |D^2 u|^2 \\& = \int_{I \times (0,1)} |\Delta u|^2 + \int_{I \times (0,1)} \sum_{i,j = 1}^2 \big( \partial_i (\partial_j u\, \partial^2_{ij} u ) -\partial_j (\partial_j u\, \partial_{ii}^2 u )\big)\\ & = \int_{I \times (0,1)} |\Delta u|^2 +\Big[\int_{I \times \{y\}} \big(\partial_j u\, \partial^2_{2j} u - \partial_2 u\, \partial^2_{ii} u\big)\,dx\Big]_{y=0}^{y = 1}\\ & = \int_{I \times (0,1)} |\Delta u|^2 +\Big[\int_{I \times \{y\}} \big(\partial_x u\, \partial^2_{xy} u - \partial_y u\, \partial^2_{xx} u\big)\,dx\Big]_{y=0}^{y = 1}. \end{align*} $$

At $y = 0,$ we get

$$ \begin{align*} \int_{I \times \{0\}} \big(\partial_x u\, \partial^2_{xy} u - \partial_y u\, \partial^2_{xx} u\big)\,dx &= \int_{I} (\varphi' \psi' - \varphi'' \psi)\,dx\\ &= -2 \sum_{k =1}^\infty k^2 \langle \varphi_k, \psi_k \rangle_{L^2(I)}. \end{align*} $$

The Cauchy–Schwarz inequality yields

$$ \begin{align*} & \Big|\int_{I \times \{0\}} \big(\partial_x u\, \partial^2_{xy} u - \partial_y u\, \partial^2_{xx} u\big)\,dx\Big| \\ & \leq 2 \Big(\sum_{k=1}^\infty k^3 \|\varphi_k\|_{L^2(I)}^2 \Big)^{\frac{1}{2}} \Big(\sum_{k=1}^\infty k \|\psi_k\|_{L^2(I)}^2 \Big)^{\frac{1}{2}}\\ & = 2 [\varphi]_{W^{\frac{3}{2},2}(I)} [\psi]_{W^{\frac{1}{2},2}(I)}. \end{align*} $$

On the other hand, standard interior estimates imply that

$$\begin{align*}\Big|\int_{I \times \{1\}} \big(\partial_x u\, \partial^2_{xy} u - \partial_y u\, \partial^2_{xx} u\big)\,dx\Big| \leq C\,(\|\varphi\|_{L^2(I)} + \|\psi\|_{L^2(I)}). \end{align*}$$

We have proved that

(A.10) $$ \begin{align} \|u\|_{C^1(I \times (0,1))} & \leq C \,\big(\|\varphi\|_{W^{1,\infty}(I)} + \|\psi\|_{L^\infty(I)}\big), \end{align} $$

(A.11) $$ \begin{align} \|u\|_{L^2(I \times (0,1))} & \leq C\,\big(\|\varphi\|_{W^{\frac{1}{2},2}(I)} + \|\psi\|_{W^{-\frac{1}{2},2}(I)}\big), \end{align} $$

(A.12) $$ \begin{align} \|D u\|_{L^2(I \times (0,1))} & \leq C\, \big([\varphi]_{W^{\frac{3}{2},2}(I)} + [\psi]_{W^{\frac{1}{2},2}(I)}\big), \end{align} $$

(A.13) $$ \begin{align} \|D^2 u\|_{L^2(I \times (0,1))} & \leq C \, \big([\varphi]_{W^{\frac{3}{2},2}(I)} + [\psi]_{W^{\frac{1}{2},2}(I)}\big). \end{align} $$

The estimate for $\|Du\|_{L^2}$ is not optimal. To conclude the proof of the lemma we choose a cutoff function $\eta \in C_c^\infty (I \times [0,1))$ such that

$$\begin{align*}\eta \equiv 1 \quad \mbox{ on } \quad \Big[-\frac{\pi}{2}, \frac{\pi}{2}\Big] \times \Big[0,\frac{1}{2}\Big]. \end{align*}$$

The function $\eta u$ has all properties required in the lemma.▪