Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T20:49:33.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Regular Homeomorphisms of Finite Order on Countable Spaces

Published online by Cambridge University Press:  20 November 2018

Yevhen Zelenyuk
Yevhen Zelenyuk*
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag 3, Wits 2050, South Africa, yevhen.zelenyuk@wits.ac.za
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a structure theorem for a broad class of homeomorphisms of finite order on countable zero dimensional spaces. As applications we show the following.

  1. (a) Every countable nondiscrete topological group not containing an open Boolean subgroup can be partitioned into infinitely many dense subsets.

  2. (b) If $G$ is a countably infinite Abelian group with finitely many elements of order 2 and 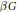$\beta G$ is the Stone–Čech compactification of $G$ as a discrete semigroup, then for every idempotent 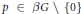$p\,\,\in \,\,\beta G\backslash \{0\}$, the subset 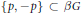$\{p,-p\}\subset \beta G$ generates algebraically the free product of one-element semigroups 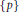$\{p\}$ and 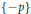$\{-p\}$.

Keywords

22A3054H1120M1554A05Homeomorphismhomogeneous spacetopological groupresolvabilityStone–Čech compactification
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 708 - 720
Copyright
Copyright © Canadian Mathematical Society2009

References

[1] Comfort, W. W. and van Mill, J., Groups with only resolvable group topologies. Proc. Amer. Math. Soc. 120(1994), 687–696.Google Scholar
[2] Hewitt, E., A problem of set-theoretic topology. Duke Math. J. 10(1943), 309–333.Google Scholar
[3] Hindman, N. and Strauss, D., Algebra in the Stone–Cech compactification. Theory and applications. de Gruyer Expositions in Mathematics 27, Walter de Gruyter, Berlin, 1998.Google Scholar
[4] Hindman, N., Leader, I., and Strauss, D., Separating Milliken-Taylor systems with negative entries. Proc. Edinb. Math. Soc. 46(2003), no. 1, 45–61.Google Scholar
[5] Malyhin, V., Extremally disconnected and similar groups. Soviet Math. Dokl. 16(1975), 21–25.Google Scholar
[6] Protasov, I. V., Indecomposable topologies on groups. Ukrainian Math. J. 50(1998), no. 12, 1879–1887.Google Scholar
[7] Zelenyuk, Y., On partitions of groups into dense subsets. Topology Appl. 126(2002), no. 1-2, 327–339.Google Scholar
[8] Zelenyuk, Y., On group operations on homogeneous spaces. Proc. Amer. Math. Soc. 132(2004), no. 4, 1219–1222.Google Scholar
[9] Zelenyuk, Y., On the ultrafilter semigroup of a topological group. Semigroup Foru. 73(2006), no. 2, 301–307.Google Scholar
[10] Zelenyuk, Y., Almost maximal spaces. Topology Appl. 154(2007), no. 2, 339–357.Google Scholar