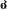Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-29T08:01:27.965Z Has data issue: false hasContentIssue false
  • English
  • Français

A Remark on Disintegrations With Almost All Components Non -Additive

Published online by Cambridge University Press:  20 November 2018

Nghiem Dang-Ngoc
Nghiem Dang-Ngoc*
Affiliation:
Université de l'Etat à Mons, Mons, Belgique
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend a theorem of L. E. Dubins on “purely finitely additive disintegrations” of measures (cf. [4]) and apply this result to the disintegrations of extremal Gibbs states with respect to the asymptotic algebra enlarging another result of L. E. Dubins on the symmetric coin tossing game.

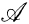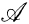We recall the following definition of L. E. Dubins (cf. [3], [4]): Let (X , , μ) be a measure space, a sub σ-algebra of . A real function σx (A), 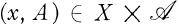is called a measurable-disintegration of μ if:

  • (i) ∀x ∊ X , σx(.) is a finitely additive measure .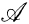

  • (ii) ∀A ∊ 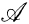, σ. (A) is constant on each -atom.

  • (iii) For each A ∊ 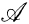, σ. (A) is measurable with respect to the completion of 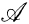by μ and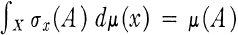

  • (iv)σx(B) = 1 if x ∊ B ∊ .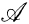

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 4 , 01 August 1979 , pp. 786 - 788
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Blackwell, D. and Dubins, L. E., On existence and non-existence of proper, regular conditional distributions, Ann. of Prob. 3 (1975), 741–753.Google Scholar
2. Dang-Ngoc, N. and Royer, G., Markov property of extremal local fields, Proc. Amer. Math. Soc. (1978), 185–188.Google Scholar
3. Dubins, L. E., Finitely additive conditional probabilities, conglomerability and disintegrations, Ann. of Prob. 3 (1975), 89–99.Google Scholar
4. Dubins, L. E., Measurable tail disintegrations of the Haar integral are purely finitely additive, Proc. Amer. Math. Soc. 62 (1977), 34–36.Google Scholar
5. Effros, E. G., Transformation groups and C*-algebras, Ann. of Math. 81 (1965), 38–55.Google Scholar
6. Follmer, H., Phase transition and Martin boundary, Séminaire de Probabilités IX. Lecture Notes in Math. (Springer-Verlag, 1975).Google Scholar
7. Georgii, H. O., Two Remarks on extremal equilibrium states, Comm. Math. Phys. 32 (1973), 107–118.Google Scholar
8. Ruelle, D., Statistical mechanics (Benjamin, New York, 1969).Google Scholar