Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-27T18:13:03.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Remetrization in Strongly Countabledimensional Spaces

Published online by Cambridge University Press:  20 November 2018

B. R. Wenner
B. R. Wenner*
Affiliation:
University of Missouri, Kansas City, Missouri
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Although the Lebesgue dimension function is topologically invariant, the dimension-theoretic properties of a metric space can sometimes be made clearer by the introduction of a new, topologically equivalent metric. A considerable amount of effort has been devoted to the problem of constructing such metrics; one example of the fruits of this research is the following theorem by Nagata (2, Theorem 5).

In order that dim R ≦ n for a metrizable space R it is necessary and sufficient to be able to define a metric p(x, y) agreeing with the topology of R such that for every ∊ > 0 and for every point x oƒ R,

imply

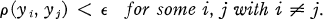
A metric ρ which satisfies the condition of this theorem is called Nagata's metric (this term was introduced, to the best of the author's knowledge, by Nagami (1, Definition 9.3)).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 748 - 750
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Nagami, K., Mappings of finite order and dimension theory, Japan. J. Math. 30 (1960), 25–54.Google Scholar
2. Nagata, J., Note on dimension theory for metric spaces, Fund. Math. 45 (1958), 143–181.Google Scholar
3. Wenner, B. R., Dimension on boundaries of e-spheres, Pacific J. Math. 27 (1968), 201—210.Google Scholar