Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T17:07:52.784Z Has data issue: false hasContentIssue false
  • English
  • Français

Representation Stability of Power Sets and Square Free Polynomials

Published online by Cambridge University Press:  20 November 2018

Samia Ashraf ,
Haniya Azam  and
Barbu Berceanu
Samia Ashraf
Affiliation:
Abdus Salam School of Mathematical Sciences, GC University, Lahore-Pakistan. e-mail: samia.ashraf@yahoo.com, centipedes.united@gmail.com
Haniya Azam
Affiliation:
Abdus Salam School of Mathematical Sciences, GC University, Lahore-Pakistan. e-mail: samia.ashraf@yahoo.com, centipedes.united@gmail.com
Barbu Berceanu
Affiliation:
Abdus Salam School of Mathematical Sciences, GC University, Lahore-Pakistan. e-mail: samia.ashraf@yahoo.com, centipedes.united@gmail.com Institute of Mathematics Simion Stoilow, Bucharest-Romania(Permanent address). e-mail: barbu.berceanu@imar.ro
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The symmetric group 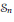${{\mathcal{S}}_{n}}$ acts on the power set 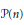$\mathcal{P}\left( n \right)$ and also on the set of square free polynomials in $n$ variables. These two related representations are analyzed from the stability point of view. An application is given for the action of the symmetric group on the cohomology of the pure braid group.

Keywords

20C3013A5020F3655R80symmetric group modulessquare free polynomialsrepresentation stabilityArnold algebra
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 5 , 01 October 2015 , pp. 1024 - 1045
Copyright
Copyright © Canadian Mathematical Society 2014

References

[A] Arnold, V. I., The cohomology ring of dyed braids. Math. Notes 5(1969), no. 2, 138–140.Google Scholar
[AAB] Ashraf, S., Azam, H., and Berceanu, B., Representation theory for the Križ model. Algebr. Geom. Topol. 14(2014), no. 1, 57–90. http://dx.doi.org/10.2140/agt.2014.14.57 Google Scholar
[C] Church, T., Homological stability for configuration spaces of manifolds. Invent. Math. 188(2012), no. 2, 465–504. http://dx.doi.org/10.1007/s00222-011-0353-4 Google Scholar
[CEF] Church, T., Ellenberg, J. S., and Farb, B., FI modules: a new approach to stability for 풮n-representations. arxiv:1204.4533v2Google Scholar
[CF] Church, T. and Farb, B., Representation theory and homological stability. arxiv:1008.1368v1Google Scholar
[FH] Fulton, W. and Harris, J., Representation theory. A first course. Graduate Texts in Mathematics, 129, Readings in Mathematics, Springer-Verlag, New York, 1991.Google Scholar
[H] Hemmer, D., Stable decompositions for some symmetric group characters arising in braid group cohomology. J. Comb. Theory Ser. A 118(2011), no. 3, 1136–1139.http://dx.doi.org/10.1016/j.jcta.2010.08.010 Google Scholar
[J] James, G. D., The representation theory of the symmetric groups. Lecture Notes in Mathematics, 682, Springer, Berlin, 1978.Google Scholar
[K] Knutson, D., λ-Rings and the representation theory of the symmetric group. Lecture Notes in Mathematics, 308, Springer-Verlag, Berlin-New York, 1973.Google Scholar
[M] Murnaghan, F. D., The analysis of the Kronecker product of irreducible representations of the symmetric group. Amer. J. Math. 60(1938), no. 3, 761–784. http://dx.doi.org/10.2307/2371610 Google Scholar
[OS] Orlik, P. and Solomon, L., Combinatorics and topology of complements of hyperplanes. Invent. Math. 56(1980), no. 2, 167–189.http://dx.doi.org/10.1007/BF01392549 Google Scholar
[S] Specht, W., Die Charaktere der symmetrischen Gruppe. Math. Z. 73(1960), 312–329. http://dx.doi.org/10.1007/BF01215313 Google Scholar
[MWW] Morita, H., Wachi, A., and Watanabe, J., Zero-dimensional Gorenstein algebras with the action of the symmetric group. Rend. Semin. Mat. Univ. Padova 121(2009), 45–71. http://dx.doi.org/10.4171/RSMUP/121-4 Google Scholar