Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-03-01T09:09:59.179Z Has data issue: false hasContentIssue false
  • English
  • Français

Représentations irréductibles bornées des groupes de Lie exponentiels

Published online by Cambridge University Press:  20 November 2018

J. Ludwig  and
C. Molitor-Braun
J. Ludwig
Affiliation:
Département de Mathématiques, Université de Metz, Ile de Saulcy, F-57045 Metz cedex 1, France. courriel: ludwig@poncelet.sciences.univ-metz.fr
C. Molitor-Braun
Affiliation:
Séminaire de mathématique, Centre Universitaire de Luxembourg, 162A, Avenue de la Faïencerie, L-1511 Luxembourg, Luxembourg. courriel: molitor@cu.lu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

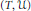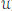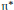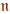Let $G$ be a solvable exponential Lie group. We characterize all the continuous topologically irreducible bounded representations $(T,\mathcal{U})$ of $G$ on a Banach space $\mathcal{U}$ by giving a $G$-orbit in ${{n}^{*}}$ ($\mathfrak{n}$ being the nilradical of 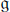$\mathfrak{g}$), a topologically irreducible representation of 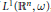${{L}^{1}}({{\mathbb{R}}^{n}},\,\,\omega )$ , for a certain weight 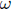$\omega $ and a certain 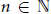$n\,\in \,\mathbb{N}$, and a topologically simple extension norm. If $G$ is not symmetric, i.e., if the weight 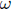$\omega $ is exponential, we get a new type of representations which are fundamentally different from the induced representations.

Résumé

Résumé

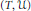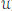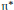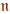Soit $G$ un groupe de Lie résoluble exponentiel. Nous caractérisons toutes les représentations $(T,\mathcal{U})$ continues bornées topologiquement irréductibles de $G$ dans un espace de Banach $\mathcal{U}$ à l’aide d’une $G$-orbite dans ${{n}^{*}}$ ($\mathfrak{n}$ étant le radical nilpotent de 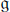$\mathfrak{g}$), d’une représentation topologiquement irréductible de 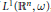${{L}^{1}}({{\mathbb{R}}^{n}},\,\,\omega )$, pour un certain poids 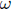$\omega $ et un certain 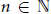$n\,\in \,\mathbb{N}$, d’une norme d’extension topologiquement simple. Si $G$ n’est pas symétrique, c. à d. si le poids 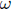$\omega $ est exponentiel, nous obtenons un nouveau type de représentations qui sont fondamentalement différentes des représentations induites.

Keywords

43A20groupe de Lie résoluble exponentielreprésentation bornée topologiquement irréductibleorbitenorme d’extensionsous-espace invariantidéal premieridéal primitif
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 5 , 01 October 2001 , pp. 944 - 978
Copyright
Copyright © Canadian Mathematical Society 2001

References

Références

[Be] Beauzamy, B., Introduction to Operator Theory and Invariant Subspaces. North-Holland Mathematical Library 42, North-Holland, Amsterdam, 1988.Google Scholar
[Ber] Bernat, P., Sur les représentations unitaires des groupes de Lie résolubles. Ann. Sci. École Norm. Sup. 82(1965), 37–99.Google Scholar
[BerCo] Bernat, P., Conze, N., Duflo, M., Lévy-Nahas, M., Rais, M., Renouard, P. et Vergne, M., Représentations des groupes de Lie résolubles. Dunod, Paris, 1972.Google Scholar
[BoDu] Bonsall, F. F. et Duncan, J., Complete Normed Algebras. Springer, New York-Heidelberg, 1973.Google Scholar
[Boi] Boidol, J., *-Regularity of Exponential Lie Groups. Invent. Math. 56(1980), 231–238.Google Scholar
[BoiLe] Boidol, J., Leptin, H., Schürman, J. et Vahle, D., Räume primitiver Ideale von Gruppenalgebren. Math. Ann. 236(1978), 1–13.Google Scholar
[CorGr] Corwin, L. et Greenleaf, F. P., Representations of nilpotent Lie groups and their applications. Cambridge University Press, Cambridge, 1990.Google Scholar
[Di1] Dixmier, J., Opérateurs de rang fini dans les représentations unitaires. Inst. Hautes Études Sci. Publ. Math. 6(1960), 305–317.Google Scholar
[Di2] Dixmier, J., Les C*-algèbres et leurs représentations. Gauthiers-Villard, Paris, 1969.Google Scholar
[FeDo] Fell, J. M. G. et Doran, R. S., Representations of ∗-Algebras, Locally Compact Groups and Banach ∗-Algebraic Bundles. Vol. 2, Academic Press, Boston, 1988.Google Scholar
[HaLu] Hauenschild, W. et Ludwig, J., The injection and the projection theorem for spectral sets. Monatsh. Math. 92(1981), 167–177.Google Scholar
[Hu] Hulanicki, A., A functional calculus for Rockland operators on nilpotent Lie groups. Studia Math. 78(1984), 253–266.Google Scholar
[Ki] Kirillov, A. A., Unitary representations of nilpotent Lie groups. Uspekhi Mat. Nauk. 17(1962), 53–104.Google Scholar
[Le] Leptin, H., Ideal Theory in Group Algebras of Locally Compact Groups. Invent. Math. 31(1976), 259–278.Google Scholar
[LeLu] Leptin, H. et Ludwig, J., Unitary Representation Theory of Exponential Lie Groups. De Gruyter Expositions in Mathematics 18, De Gruyter, Berlin, 1994.Google Scholar
[Lu1] Ludwig, J., Polynomial growth and ideals in group algebras. Manuscr. Math. 30(1980), 215–221.Google Scholar
[Lu2] Ludwig, J., Irreducible representations of exponential solvable Lie groups and operators with smooth kernels. J. Reine Angew. Math. 339(1983), 1–26.Google Scholar
[Lu3] Ludwig, J., On Primary Ideals in the Group Algebra of a Nilpotent Lie Group. Math. Ann. 262(1983), 287–304.Google Scholar
[Lu4] Ludwig, J., Minimal C*-dense ideals and algebraically irreducible representations of the Schwartz-algebra of a nilpotent Lie group. Harmonic Analysis (Luxembourg, 1987), Springer Lecture Notes in Math. 1359(1988), 209–217.Google Scholar
[LuMo1] Ludwig, J. et Molitor-Braun, C., L’algèbre de Schwartz d’un groupe de Lie nilpotent. Travaux mathématiques VII, Sém. Math. Luxembourg, 1995, 25–67.Google Scholar
[LuMo2] Ludwig, J. et Molitor-Braun, C., Exponential actions, orbits and their kernels. Bull. Austral. Math. Soc. 57(1998), 497–513.Google Scholar
[LuRoSa] Ludwig, J., Rosenbaum, G. et Samuel, J., The elements of bounded trace in the C*-algebra of a nilpotent Lie group. Invent.Math. 83(1986), 167–190.Google Scholar
[Mo1] Molitor-Braun, C., Actions exponentielles et idéaux premiers. Thèse, Metz, 1996.Google Scholar
[Mo2] Molitor-Braun, C., Exponential actions and maximal -invariant ideals. Manuscr. Math. 96(1998), 23–35.Google Scholar
[Pa] Palmer, T. W., Banach Algebras and the General Theory of ∗-Algebras. Vol. I, Algebras and Banach Algebras, Encyclopedia of Mathematics and its Applications, Vol. 49, Cambridge University Press, Cambridge, 1994.Google Scholar
[Pi] Pier, J. P., Amenable Locally Compact Groups. J. Wiley and Sons, New York, 1984.Google Scholar
[Po1] Poguntke, D., Operators of Finite Rank in Unitary Representations of Exponential Lie Groups. Math. Ann. 259(1982), 371–383.Google Scholar
[Po2] Poguntke, D., Algebraically irreducible representations of L 1 -algebras of exponential Lie groups. Duke Math. J. (4) 50(1983), 1077–1106.Google Scholar
[Pu] Pukanszky, L., On the Unitary Representations of Exponential Groups. J. Funct. Anal. 2(1968), 73–113.Google Scholar
[So] Soergel, W., An irreducible not admissible Banach representation of SL(2, ℝ) . Proc. Amer. Math. Soc. (4) 104(1988), 1322–1324.Google Scholar