Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T02:08:30.522Z Has data issue: false hasContentIssue false
  • English
  • Français

Representations of Well-Founded Preference Orders

Published online by Cambridge University Press:  20 November 2018

Douglas Cenzer  and
R. Daniel Mauldin
Douglas Cenzer
Affiliation:
University of Florida, Gainsville, Florida
R. Daniel Mauldin
Affiliation:
North Texas State University, Denton, Texas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A preference order, or linear preorder, on a set X is a binary relation 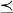which is transitive, reflexive and total. This preorder partitions the set X into equivalence classes of the form 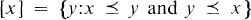. The natural relation induced by 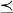on the set of equivalence classes is a linear order. A well-founded preference order, or prewellordering, will similarly induce a well-ordering. A representation or Paretian utility function of a preference order is an order-preserving map f from X into the R of real numbers (provided with the standard ordering). Mathematicians and economists have studied the problem of obtaining continuous or measurable representations of suitably defined preference orders [4, 7]. Parametrized versions of this problem have also been studied [1, 7, 8]. Given a continuum of preference orders which vary in some reasonable sense with a parameter t, one would like to obtain a continuum of representations which similarly vary with t.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 3 , 01 June 1983 , pp. 496 - 508
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Burgess, J. P., From preference to utility, A problem of descriptive set theory, Notre Dame Journal of Formal Logic, to appear.CrossRefGoogle Scholar
2. Burgess, J. P., A reflection phenomenon, Fund. Math. 104 (1979), 128–139.Google Scholar
3. Cenzer, D. and Mauldin, R. D., Inductive definability, measure and category, Advances in Math. 38 (1980), 55–90.Google Scholar
4. Debreu, G., Continuity properties of Paretian utility, Int'l. Econ. Review 5 (1964), 285–293.Google Scholar
5. Faden, A. M., Economics of space and time, The Measure-theoretic Foundations of Social Science (Iowa State U. Press, 1977).Google Scholar
6. Kuratowski, K., Topology, Vol. I (Acad. Press, 1966).Google Scholar
7. Mauldin, R. D., Measurable representations of preference orders, Trans. Amer. Math. Soc. 275 (1983), 761–769.Google Scholar
8. Wesley, E., Borel preference orders in markets with a continuum of traders, J. Math. Economics 3 (1976), 155–165.Google Scholar