Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jain, S. K.
and
Singh, Surjeet
1969.
Rings having one-sided ideals satisfying a polynomial identity.
Archiv der Mathematik,
Vol. 20,
Issue. 1,
p.
17.
Martindale, Wallace S
1969.
Rings with involution and polynomial identities.
Journal of Algebra,
Vol. 11,
Issue. 2,
p.
186.
Montgomery, Susan
1971.
A generalization of a theorem of Jacobson.
Proceedings of the American Mathematical Society,
Vol. 28,
Issue. 2,
p.
366.
Montgomery, Susan
1971.
Polynomial identity algebras with involution.
Proceedings of the American Mathematical Society,
Vol. 27,
Issue. 1,
p.
53.
Osborn, J.Marshall
1972.
Varieties of algebras.
Advances in Mathematics,
Vol. 8,
Issue. 2,
p.
163.
Montgomery, Susan
1972.
Algebraic algebras with involution.
Proceedings of the American Mathematical Society,
Vol. 31,
Issue. 2,
p.
368.
Bokut’, L. A.
Zhevlakov, K. A.
and
Kuz’min, E. N.
1972.
Algebra and Geometry.
Vol. 12,
Issue. ,
p.
3.
Burgess, W.D
and
Chacron, M
1973.
A generalization of a theorem of Herstein and montgomery.
Journal of Algebra,
Vol. 27,
Issue. 1,
p.
31.
Loustau, J.A
1974.
Radical extensions of Jordan rings.
Journal of Algebra,
Vol. 30,
Issue. 1-3,
p.
1.
Rowen, Louis Halle
1975.
Generalized polynomial identities.
Journal of Algebra,
Vol. 34,
Issue. 3,
p.
458.
Rowen, Louis Halle
1975.
Identities in algebras with involution.
Israel Journal of Mathematics,
Vol. 20,
Issue. 1,
p.
70.
Loustau, J.A.
1976.
The structure of algebraic jordan algebras without nonzero nilpotent elements.
Communications in Algebra,
Vol. 4,
Issue. 11,
p.
1045.
Rowen, Louis Halle
1977.
Generalized polynomial identities, III.
Journal of Algebra,
Vol. 46,
Issue. 2,
p.
305.
Baxter, W.E
and
Casciotti, L.A
1978.
A condition of Brauer-Cartan-Hua type-II.
Journal of Algebra,
Vol. 55,
Issue. 2,
p.
481.
Loustau, J. A.
1978.
On algebraic power-associative and Jordan algebras with semi-normal functionals.
Manuscripta Mathematica,
Vol. 24,
Issue. 4,
p.
379.
Beidar, K. I.
and
T�n, V. D.
1978.
The local finiteness of some PI-algebras.
Siberian Mathematical Journal,
Vol. 18,
Issue. 4,
p.
663.
Osborn, J.Marshall
and
Racine, Michel
1980.
Prime Jordan P.I. Algebras with nonzero socle and Jordan division algebras.
Journal of Algebra,
Vol. 62,
Issue. 2,
p.
249.
1980.
Polynomial Identities in Ring Theory.
Vol. 84,
Issue. ,
p.
341.

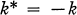 , and
, and 