Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-15T07:20:12.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Screenability, Pointwise Paracompactness, and Metrization of Moore Spaces

Published online by Cambridge University Press:  20 November 2018

R. W. Heath
R. W. Heath*
Affiliation:
University of Georgia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

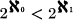F. B. Jones (6) has shown that, if , then every separable normal Moore space is metrizable. It is not known whether this assumption is necessary, though perhaps some progress is made in (5). However, it is easily seen from R. H. Bing's Example E in (3) that a certain condition (see (1) below) implied by 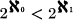is necessary. Also in (3), Bing showed that every screenable normal Moore space is metrizable. In this paper we establish that: (1) every separable normal Moore space is metrizable if and only if every uncountable subspace M of E1 contains a subset which is not an Fσ (in M); (2) if every pointwise paracompact normal Moore space is metrizable, then so is every separable normal Moore space; (3) every screenable Moore space is pointwise paracompact but not conversely; (4) a T3-space is a pointwise paracompact Moore space if and only if it has a uniform base (in the sense of (1, p. 40), not a uniformity).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 16 , 1964 , pp. 763 - 770
Copyright
Copyright © Canadian Mathematical Society 1964

References

1. Aleksandrov, P. S., Some results in the theory of topological spaces, obtained within the last twenty-five years, Russian Math. Surveys, 15 (1960), 23–83.Google Scholar
2. Bing, R. H., Extending a metric, Duke Math. J., 14 (1947), 511–519.Google Scholar
3. Bing, R. H., Metrization of topological spaces, Can. J. Math., 3 (1951), 175–186.Google Scholar
4. Grace, E. E. and Heath, R. W., Separability and metrizability in pointwise paracompact Moore spaces, Duke Math. J., to appear.Google Scholar
5. Heath, R. W., Separability and א-compactness, Coll. Math., 12 (1964), 11–14.Google Scholar
6. Jones, F. B., Concerning normal and completely normal spaces, Bull. Amer. Math. Soc, 48 (1937), 671–677.Google Scholar
7. Kelley, J. L., General topology (Princeton, 1955).Google Scholar
8. McAuley, L. F., A relation between perfect separability, completeness, and normality in semi-metric spaces, Pacific J. Math., 6 (1956), 315–326.Google Scholar
9. Moore, R. L., Foundations of point set theory, Am. Math. Soc. Coll. Publ., 13 (New York, 1932).Google Scholar
10. Traylor, D. R., Concerning metrizability in pointwise paracompact Moore spaces. Can. J. Math., 16 (1964), 407–411.Google Scholar