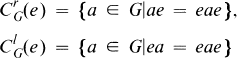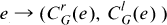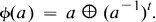Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Renner, Lex E.
1987.
Connected algebraic monoids.
Semigroup Forum,
Vol. 36,
Issue. 1,
p.
365.
Putcha, M.S
and
Renner, L.E
1988.
The system of idempotents and the lattice of I-classes of reductive algebraic monoids.
Journal of Algebra,
Vol. 116,
Issue. 2,
p.
385.
Putcha, Mohan S
1989.
Monoids on groups with BN-Pairs.
Journal of Algebra,
Vol. 120,
Issue. 1,
p.
139.
Cohen, Jo-Ann
and
Koh, Kwangil
1996.
Idempotents in a compact ring.
Communications in Algebra,
Vol. 24,
Issue. 11,
p.
3653.


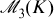 denote the monoid of all 3 × 3 matrices over K. If e is an idempotent in
denote the monoid of all 3 × 3 matrices over K. If e is an idempotent in