Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-16T00:27:42.824Z Has data issue: false hasContentIssue false
  • English
  • Français

Sieve-Generated Sequences with Translated Intervals

Published online by Cambridge University Press:  20 November 2018

R. G. Buschman  and
M. C. Wunderlich
R. G. Buschman
Affiliation:
State University of New York, Buffalo
M. C. Wunderlich
Affiliation:
State University of New York, Buffalo
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the following sieve process. Let A(1) be the sequence of integers greater than 1. Let A(n+1) be obtained from A(n) = {a1(n), a2(n), …} by eliminating one element from each of the intervals Ik(n), where

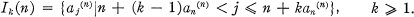
We let an = an(n) and A = {an} be the sequence of integers that survive the sieve. M. C. Wunderlich (8) has found a necessary and sufficient condition for an ∼ n log n and, in a more recent paper, M. Wunderlich and W. E. Briggs (9) have studied a subclass of the sequences defined above for which an ∼ n log n.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 559 - 570
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Briggs, W. E., Prime-like sequences generated by a sieve process, Duke Math. J., 30 (1963), 297–312.Google Scholar
2. Buschman, R. G. and Wunderlich, M. C., Sieves with generalized intervals, Boll. Un. Mat. Ital. (to appear).Google Scholar
3. Erdos, P. and Jabotinsky, E., On sequences generated by a sieving process, Nederl. Akad. Wetensch. Indag. Math., 61 (1958), 115–128.Google Scholar
4. Gardiner, V., Lazarus, R., Metropolis, M., and Ulam, S., On certain sequences of integers defined by sieves, Math. Mag., 29 (1955/56), 117–122.Google Scholar
5. Hawkins, D., The random sieve, Math. Mag., 81 (1957/58), 1–3.Google Scholar
6. Hawkins, D. and Briggs, W. E., The lucky number theorem, Math. Mag., 31 (1957/58), 277–280.Google Scholar
7. Lachapelle, B., L'Espérance mathématique du nombre de nombres premiers aléatoires inférieurs ouegualàx, Can. Math. Bull., 4 (1961), 139–142.Google Scholar
8. Wunderlich, M. C., Sieve-generated sequences, Can. J. Math., 18 (1966), 291–299.Google Scholar
9. Wunderlich, M. C. and Briggs, W. E., Second and third term approximations of sieve-generated sequences, Illinois J. Math., 10 (1966), 694–700.Google Scholar