Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T02:32:38.663Z Has data issue: false hasContentIssue false
  • English
  • Français

Similarity Classification of Cowen-Douglas Operators

Published online by Cambridge University Press:  20 November 2018

Chunlan Jiang
Chunlan Jiang*
Affiliation:
Department of Mathematics, Hebei Normal University, Shijiazhuang 050016, P.R. China e-mail: cljiang@mail.hebtu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

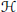Let $\mathcal{H}$ be a complex separable Hilbert space and 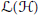$\mathcal{L}\left( \mathcal{H} \right)$ denote the collection of bounded linear operators on 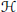$\mathcal{H}$. An operator 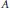$A$ in 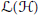$\mathcal{L}\left( \mathcal{H} \right)$ is said to be strongly irreducible, if 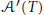${{\mathcal{A}}^{\prime }}(T)$, the commutant of 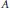$A$, has no non-trivial idempotent. An operator 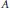$A$ in 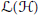$\mathcal{L}\left( \mathcal{H} \right)$ is said to be a Cowen-Douglas operator, if there exists 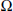$\Omega $, a connected open subset of 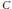$C$, and $n$, a positive integer, such that

  1. (a)

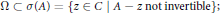    $$\Omega \,\subset \,\sigma (A)\,=\,\left\{ z\,\in \,C|\,A-z\,\text{not}\,\text{invertible} \right\};$$

  2. (b)

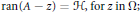    $$\text{ran(A}-z\text{)}\,\text{=}\,\mathcal{H}\text{,}\,\text{for}\,z\,\text{in}\,\Omega \text{;}$$

  3. (c)

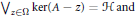    $${{\vee }_{z\in \Omega }}\,\ker (A-\,z)\,=\,\mathcal{H}\,\text{and}$$

  4. (d)

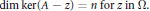    $$\dim\,\ker (A-z)\,=\,n\,\text{for}\,z\,\text{in}\,\Omega $$

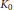In the paper, we give a similarity classification of strongly irreducible Cowen-Douglas operators by using the ${{K}_{0}}$-group of the commutant algebra as an invariant.

Keywords

47A1547C1513E0513F05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 4 , 01 August 2004 , pp. 742 - 775
Copyright
Copyright © Canadian Mathematical Society 2004

References

[Ap-Do-Fo] Apostol, C., Douglas, R. G. and Fioas, C., Quasisimilar models for nilpotent operators. Trans. Amer. Math. Soc. 224(1976), 407–415.Google Scholar
[Ap-Fi-He-Vo] Apostol, C., Fialkow, L. A., Herrero, D. A. and Voiculescu, D., Approximation of Hilbert space operator II. Research Notes in Mathematics, 102, Pitman, Boston, MA, 1984.Google Scholar
[Au] Aupetit, B., A primer on spectral theory. Springer-Verlag, Berlin, 1991.Google Scholar
[Ba] Blackadar, B., K-theory for operator algebras. Springer-Verlag, New York, 1986.Google Scholar
[Ca-Fa-Ji] Cao, Y., Fang, J. S. and Jiang, C. L., K-Group of Banach algebra and strongly irreducible decomposition of operators. J. Operator Theory (to appear).Google Scholar
[Co] Conway, J. B., Subnormal operators. Research Notes in Mathematics, 51, Pitman, Boston, MA, 1981.Google Scholar
[Co-Do] Cowen, M. J. and Douglas, R. G., Complex geometry and operator theory. Acta Math. 141 (1978), 187–261.Google Scholar
[Da-He] Davidson, K. R. and Herrero, D. A., The Jordan form of a bitriangular operator. J. Funct. Anal. 94(1990), 27–73.Google Scholar
[Do] Douglas, R. G., Banach algebra techniques in operator theory. Academic Press, New York, 1972.Google Scholar
[Fo-Ji] Fong, C. K. and Jiang, C. L., Approximation by Jordan type operators. Houston J. Math. 19(1993), 51–62.Google Scholar
[Gr] Grauert, H., Analytische faserungen über holomorph vollstandigen räumen. Math. Ann. 135(1958), 263–273.Google Scholar
[Gi] Gilfeather, F., Strong reducibility of operators. Indiana Univ. Math. J. 22(1972), 393–397.Google Scholar
[Ha] Halmos, P. R., A Hilbert space problem book. Van Nostrand, Princeton, NJ, 1967.Google Scholar
[He1] Herrero, D. A., Spectral pictures of operators in the Cowen-Douglas class ℬ n (Ω) and its closure. J. Operator Theory 18(1987), 213–222.Google Scholar
[He2] Herrero, D. A., Approximation of Hilbert space operators, I. 2nd ed. Research Notes in Mathematics, 224, Longman, Harlow, 1990.Google Scholar
[Ji1] Jiang, Z. J., Topics in operator theory. Seminar Reports in Functional Analysis, Jilin University, 1979, Changchun (in Chinese).Google Scholar
[Ji-Wa] Jiang, C. L. and Wang, Z. Y., Strongly irreducible operators on Hilbert space. Research Notes in Mathematics, 389, Longman, Harlow, 1998.Google Scholar
[Ka] Kato, T., Perturbation theory of linear operators. Grundlehren Math. Wiss. 132(1966).Google Scholar
[Su] Šubin, M. A., Factorization of matrix functions dependent on a parameter in normed rings, and related questions in the theory of Noetherian operators. Mat. Sb. 113(1967), 610–629.Google Scholar