No CrossRef data available.
Article contents
Simultaneously preperiodic points for a family of polynomials in positive characteristic
Published online by Cambridge University Press: 12 December 2024
Abstract
In the goundbreaking paper [BD11] (which opened a wide avenue of research regarding unlikely intersections in arithmetic dynamics), Baker and DeMarco prove that for the family of polynomials 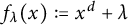 $f_\lambda (x):=x^d+\lambda $ (parameterized by
$f_\lambda (x):=x^d+\lambda $ (parameterized by 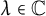 $\lambda \in \mathbb {C}$), given two starting points a and b in
$\lambda \in \mathbb {C}$), given two starting points a and b in 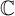 $\mathbb {C}$, if there exist infinitely many
$\mathbb {C}$, if there exist infinitely many 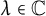 $\lambda \in \mathbb {C}$ such that both a and b are preperiodic under the action of
$\lambda \in \mathbb {C}$ such that both a and b are preperiodic under the action of 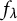 $f_\lambda $, then
$f_\lambda $, then 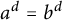 $a^d=b^d$. In this paper, we study the same question, this time working in a field of characteristic
$a^d=b^d$. In this paper, we study the same question, this time working in a field of characteristic 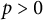 $p>0$. The answer in positive characteristic is more nuanced, as there are three distinct cases: (i) both starting points a and b live in
$p>0$. The answer in positive characteristic is more nuanced, as there are three distinct cases: (i) both starting points a and b live in 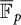 ${\overline {\mathbb F}_p}$; (ii) d is a power of p; and (iii) not both a and b live in
${\overline {\mathbb F}_p}$; (ii) d is a power of p; and (iii) not both a and b live in 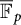 ${\overline {\mathbb F}_p}$, while d is not a power of p. Only in case (iii), one derives the same conclusion as in characteristic
${\overline {\mathbb F}_p}$, while d is not a power of p. Only in case (iii), one derives the same conclusion as in characteristic 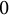 $0$ (i.e., that
$0$ (i.e., that 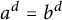 $a^d=b^d$). In case (i), one has that for each
$a^d=b^d$). In case (i), one has that for each 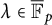 $\lambda \in {\overline {\mathbb F}_p}$, both a and b are preperiodic under the action of
$\lambda \in {\overline {\mathbb F}_p}$, both a and b are preperiodic under the action of 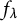 $f_\lambda $, while in case (ii), one obtains that also whenever
$f_\lambda $, while in case (ii), one obtains that also whenever 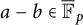 $a-b\in {\overline {\mathbb F}_p}$, then for each parameter
$a-b\in {\overline {\mathbb F}_p}$, then for each parameter 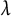 $\lambda $, we have that a is preperiodic under the action of
$\lambda $, we have that a is preperiodic under the action of 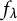 $f_\lambda $ if and only if b is preperiodic under the action of
$f_\lambda $ if and only if b is preperiodic under the action of 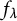 $f_\lambda $.
$f_\lambda $.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society


