Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-13T07:55:47.127Z Has data issue: false hasContentIssue false
  • English
  • Français

A Skew Hadamard Matrix of Order 52

Published online by Cambridge University Press:  20 November 2018

D. Blatt  and
G. Szekeres
D. Blatt
Affiliation:
University of Sydney, Sydney, Australia
G. Szekeres
Affiliation:
University of New South Wales, Kensington, New South Wales
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. A Hadamard (H-) matrix H = (hij) of order n is an n × n square matrix satisfying the conditions

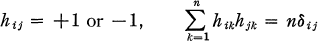
for all i, j ≦ n. A skew H-matrix is an H-matrix of the form

where I is the identity matrix and S’ the transpose of 5. In particular,

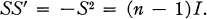
Skew H-matrices have applications in the theory of finite projective planes (2) and tournaments (4), also in the construction of H-matrices of certain orders. For example, if there is a skew H-matrix of order n, then there is an H-matrix of order n(n – 1) (Williamson, see (1, p. 213)).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1319 - 1322
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Hall, Marshall, Jr., Combinatorial theory (Blaisdell, Waltham, Massachusetts, 1967).Google Scholar
2. Johnsen, E. C., Integral solutions to the incidence equation for finite projective plane cases of orders n = 2 (mod 4), Pacific J. Math. 17 (1966), 97–120 Google Scholar
3. Paley, R. E. A. C., On orthogonal matrices, J. Math. Phys. 12 (1933), 311–320.Google Scholar
4. Szekeres, G., Tournaments and Hadamard matrices, Enseignement Math. 15 (1969), 269–278.Google Scholar
5. Williamson, J., Hadamard's determinant theorem and the sum of four squares, Duke Math. J. 11 (1944), 65–81.Google Scholar