Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T13:54:15.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Solvable Points on Projective Algebraic Curves

Published online by Cambridge University Press:  20 November 2018

Ambrus Pál
Ambrus Pál*
Affiliation:
Centre de recherches mathématiques, Université e Montréal, C.P. 6128, Succ. Centre-ville, Montréal, Quebec, H3C3J7 e-mail: pal@math.mcgill.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We examine the problem of finding rational points defined over solvable extensions on algebraic curves defined over general fields. We construct non-singular, geometrically irreducible projective curves without solvable points of genus $g$, when $g$ is at least 40, over fields of arbitrary characteristic. We prove that every smooth, geometrically irreducible projective curve of genus 0, 2, 3 or 4 defined over any field has a solvable point. Finally we prove that every genus 1 curve defined over a local field of characteristic zero with residue field of characteristic 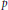$p$ has a divisor of degree prime to 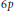$6p$ defined over a solvable extension.

Keywords

14H2511D88
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 3 , 01 June 2004 , pp. 612 - 637
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Curtis, C. W. and Reiner, I., Methods of representation theory, vol I. John Wiley & Sons, Inc., New York, 1981.Google Scholar
[2] Deligne, P. and Mumford, D., The irreducibility of the space of curves of given genus. Publ. Math. IHES 36(1969), 75–109.Google Scholar
[3] Harbater, D.,Mock covers and Galois extensions. J. Algebra 91(1984), 281–293.Google Scholar
[4] Hartshorne, R., Algebraic geometry. Springer-Verlag, New York, Berlin, 1977.Google Scholar
[5] Jouanolou, J.-P., Théorèmes de Bertini et applications. Birkhäuser, Boston, Basel, Stuttgart, 1983.Google Scholar
[6] Katz, N. and Mazur, B., Arithmetic moduli of elliptic curves. Princeton University Press, Princeton, 1985.Google Scholar
[7] Kollár, J., Rational curves on algebraic varieties. Springer-Verlag, New York, Berlin, 1996.Google Scholar
[8] Manin, Yu. I., Cubic forms: algebra, geometry, arithmetic. North-Holland Publishing Company, Amsterdam, 1974.Google Scholar
[9] Merkurjev, A. S. and Suslin, A. S., K-cohomology of Severi-Brauer varieties and the norm residue homomorphism. Izv. Akad. Nauk SSSR Ser.Mat. 46(1982), 1011–1046.Google Scholar
[10] Milne, J., Étale cohomology. Princeton University Press, Princeton, New Jersey, 1980.Google Scholar
[11] Serre, J.-P., Corps locaux. Hermann, Paris, 1962.Google Scholar
[12] Silverman, J., Advanced topics in the arithmetic of elliptic curves. Springer-Verlag, New York, Berlin, 1994.Google Scholar
[13] Weil, A., Adéles and algebraic groups. Birkhäuser, Boston, Basel, Stuttgart, 1982.Google Scholar