Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Branges, Louis
1963.
A comparison theorem for spaces of entire functions.
Proceedings of the American Mathematical Society,
Vol. 14,
Issue. 3,
p.
490.
de Branges, Louis
1964.
New and old problems for entire functions.
Bulletin of the American Mathematical Society,
Vol. 70,
Issue. 2,
p.
214.
de Branges, Louis
1965.
Some Hilbert spaces of analytic functions. III.
Journal of Mathematical Analysis and Applications,
Vol. 12,
Issue. 2,
p.
149.
de Branges, Louis
1965.
Some Hilbert spaces of analytic functions. II.
Journal of Mathematical Analysis and Applications,
Vol. 11,
Issue. ,
p.
44.
Trutt, David
1967.
Extremal norm-determining measures for Hilbert spaces of entire functions.
Journal of Mathematical Analysis and Applications,
Vol. 20,
Issue. 1,
p.
74.
1973.
Introduction to the Theory of Entire Functions.
Vol. 56,
Issue. ,
p.
186.
Mitkovski, Mishko
and
Poltoratski, Alexei
2010.
Pólya sequences, Toeplitz kernels and gap theorems.
Advances in Mathematics,
Vol. 224,
Issue. 3,
p.
1057.
Baranov, Anton
Belov, Yurii
and
Borichev, Alexander
2012.
A restricted shift completeness problem.
Journal of Functional Analysis,
Vol. 263,
Issue. 7,
p.
1887.
Mitkovski, Mishko
and
Poltoratski, Alexei
2015.
On the determinacy problem for measures.
Inventiones mathematicae,
Vol. 202,
Issue. 3,
p.
1241.
Poltoratski, A.
2021.
Nine Mathematical Challenges.
Vol. 104,
Issue. ,
p.
133.


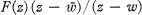 is in the space and has the same norm as
is in the space and has the same norm as 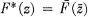 is in the space and has the same norm as
is in the space and has the same norm as 