Article contents
Some Finiteness Conditions for Orthomodular Lattices
Published online by Cambridge University Press: 20 November 2018
Extract
Throughout this paper L will be an orthomodular lattice and 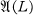 the set of all maximal Boolean subalgebras, also called blocks [4], of L. For every x ∈ L, C(x) will be the set of all elements of L which commute with x. Let n ≧ 1 be a natural number. In this paper we consider the following conditions for L:
the set of all maximal Boolean subalgebras, also called blocks [4], of L. For every x ∈ L, C(x) will be the set of all elements of L which commute with x. Let n ≧ 1 be a natural number. In this paper we consider the following conditions for L:
An: L has at most n blocks,
Bn: there exists a covering of L by at most n blocks,
Cn: the set ﹛C(x)| x ∈ L﹜ has at most n elements,
Dn: out of any n + 1 elements of L at least two commute.
We also consider quantified versions of these statements, namely the statements A, B, C, D defined by: A ⇔ ∃ nAn, B ⇔ ∃ nBn, C ⇔ ∃ nCn and D ⇔ ∃ nDn.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1982
References
- 8
- Cited by


