Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T01:23:38.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Generalizations of Ramanujan's Sum

Published online by Cambridge University Press:  20 November 2018

K. G. Ramanathan  and
M. V. Subbarao
K. G. Ramanathan
Affiliation:
Tata Institute of Fundamental Research, Bombay, India
M. V. Subbarao
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Ramanujan's well known trigonometrical sum C(m, n) denned by

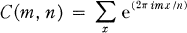
where x runs through a reduced residue system (mod n), had been shown to occur in analytic problems concerning modular functions of one variable, by Poincaré [4]. Ramanujan, independently later, used these trigonometrical sums in his remarkable work on representation of integers as sums of squares [6]. There are various generalizations of C(m, n) in the literature (some also to algebraic number fields); see, for example, [9] which gives references to some of these. Perhaps the earliest generalization to algebraic number fields is due to H. Rademacher [5]. We here consider a novel generalization involving matrices.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 5 , 01 October 1980 , pp. 1250 - 1260
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Braun, H., Hermitian modular functions, Annals of Math. 50 (1949), 829–855.Google Scholar
2. Christian, U., Über teiterfreude symmetrische Matrizenpaare, J. fur. Math. 22 (1968), 43–49.Google Scholar
3. Hardy, G. H., Ramanujan (Cambridge, 1940).Google Scholar
4. Poincaré, H., Fonctions modulaires et jonctions Fuchsiennes, Ouevres. T2, 592–618.Google Scholar
5. Rademacher, H., Zur additiven Frimzahltheorie algebrischer zahlkörper III, Math. Zeit. 27 (1928), 321–426.Google Scholar
6. Ramanujan, S., Collected Papers (Cambridge, 1927), 179–199.Google Scholar
7. Siegel, C. L., Einfùhrung in die Théorie der Modulfunktionen n-ten Grades, Math. Annalen 116 (1939), 617–657.Google Scholar
8. Siegel, C. L., Über die analytische Théorie der quadratischen Formen, Ann. of Math, 36 (1935), 527–606.Google Scholar
9. Subbarao, M. V. and Harris, V. C., A new generalization of Ramanujan's sum, J. London Math. Soc. 41 (1966), 595–604.Google Scholar