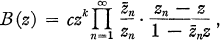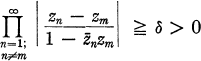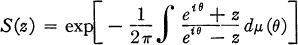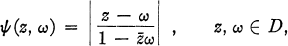Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1970.
Theory of Hp Spaces.
Vol. 38,
Issue. ,
p.
237.
Øyma, Knut
1977.
Extremal interpolatory functions in 𝐻^{∞}.
Proceedings of the American Mathematical Society,
Vol. 64,
Issue. 2,
p.
272.
1981.
Bounded Analytic Functions.
Vol. 96,
Issue. ,
p.
444.
Guillory, Carroll J
1987.
Douglas algebras of the form H∞[q̄].
Journal of Mathematical Analysis and Applications,
Vol. 126,
Issue. 1,
p.
269.
Laroco, Leonardo A.
1991.
Stable rank and approximation theorems in 𝐻^{∞}.
Transactions of the American Mathematical Society,
Vol. 327,
Issue. 2,
p.
815.
Martin, Reiner
1992.
On the ideal structure of the Nevanlinna class.
Proceedings of the American Mathematical Society,
Vol. 114,
Issue. 1,
p.
135.
Nicolau, Artur
1994.
Interpolating Blaschke products solving Pick-Nevanlinna problems.
Journal d'Analyse Mathématique,
Vol. 62,
Issue. 1,
p.
199.
Mortini, Raymond
and
Nicolau, Artur
2004.
Frostman shifts of inner functions.
Journal d'Analyse Mathématique,
Vol. 92,
Issue. 1,
p.
285.
Cichoń, Kinga
2005.
Closed range multiplication operators on weighted Bergman spaces.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 60,
Issue. 1,
p.
37.
Gorkin, Pamela
and
Mortini, Raymond
2005.
Cluster sets of interpolating Blaschke products.
Journal d'Analyse Mathématique,
Vol. 96,
Issue. 1,
p.
369.
Gorkin, Pamela
and
Mortini, Raymond
2005.
Radial limits of interpolating Blaschke products.
Mathematische Annalen,
Vol. 331,
Issue. 2,
p.
417.
Gorkin, Pamela
Mortini, Raymond
and
Nikolski, Nikolai
2008.
Norm controlled inversions and a corona theorem for H∞-quotient algebras.
Journal of Functional Analysis,
Vol. 255,
Issue. 4,
p.
854.
Gorkin, Pamela
and
Mortini, Raymond
2010.
Two new characterizations of carleson-newman Blaschke products.
Israel Journal of Mathematics,
Vol. 177,
Issue. 1,
p.
267.
Heittokangas, Janne
2011.
On Interpolating Blaschke Products and Blaschke-Oscillatory Equations.
Constructive Approximation,
Vol. 34,
Issue. 1,
p.
1.
Mortini, Raymond
2011.
A New Class of Inner Functions Uniformly Approximable by Interpolating Blaschke Products.
Complex Analysis and Operator Theory,
Vol. 5,
Issue. 1,
p.
219.
Gröhn, Janne
and
Heittokangas, Janne
2012.
New Findings on the Bank–Sauer Approach in Oscillation Theory.
Constructive Approximation,
Vol. 35,
Issue. 3,
p.
345.
Guo, Kunyu
and
Huang, Hansong
2014.
Geometric constructions of thin Blaschke products and reducing subspace problem.
Proceedings of the London Mathematical Society,
Vol. 109,
Issue. 4,
p.
1050.
Guo, Kunyu
and
Huang, Hansong
2015.
Multiplication Operators on the Bergman Space.
Vol. 2145,
Issue. ,
p.
7.
Akeroyd, John R.
and
Gorkin, Pamela
2016.
Uniform approximation by indestructible Blaschke products.
Journal of Mathematical Analysis and Applications,
Vol. 434,
Issue. 2,
p.
1419.
Cima, Joseph
and
Mortini, Raymond
2017.
One-component inner functions.
Complex Analysis and its Synergies,
Vol. 3,
Issue. 1,