No CrossRef data available.
Article contents
Some New Results on L2 Cohomology of Negatively Curved Riemannian Manifolds
Published online by Cambridge University Press: 20 November 2018
Abstract
The present paper is concerned with the study of the 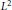 ${{L}^{2}}$ cohomology spaces of negatively curved manifolds. The first half presents a finiteness and vanishing result obtained under some curvature assumptions, while the second half identifies a class of metrics having non-trivial
${{L}^{2}}$ cohomology spaces of negatively curved manifolds. The first half presents a finiteness and vanishing result obtained under some curvature assumptions, while the second half identifies a class of metrics having non-trivial 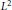 ${{L}^{2}}$ cohomology for degree equal to the half dimension of the space. For the second part we rely on the existence and regularity properties of the solution for the heat equation for forms.
${{L}^{2}}$ cohomology for degree equal to the half dimension of the space. For the second part we rely on the existence and regularity properties of the solution for the heat equation for forms.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2005


