Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T10:26:06.364Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Order Properties of the Lattice of Varieties of Commutative Semigroups

Published online by Cambridge University Press:  20 November 2018

Jorge Almeida
Jorge Almeida*
Affiliation:
Universidade do Minho, Braga, Portugal Simon Fraser University, Burnaby, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The most complete work on the structure of the lattice 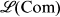of varieties of commutative semigroups available to this date is [12]. Nevertheless, it fails to give the structure of this lattice. In the positive direction, it shows in particular that the order structure of 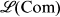is determined by the order structure of well-known lattices of integers together with the sublattice 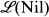of varieties of commutative nil semigroups.

In the present work, we study 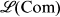from the point of view of order. Perkins [13] has shown that 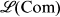has no infinite descending chains and is countable. The underlying questions we consider here arose from the results of Almeida and Reilly [1] in connection with generalized varieties. There, it is observed that the best-known part of 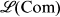consisting of the varieties all of whose elements are abelian groups is in a sense very wide: it contains infinite subsets of mutually incomparable elements and allows the construction of uncountably many generalized varieties and infinite descending chains of generalized varieties.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 1 , 01 February 1986 , pp. 19 - 47
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Almeida, J. and Reilly, N. R., Generalized varieties of commutative and nilpotent semigroups, Semigroup Forum 30 (1984), 77–98.Google Scholar
2. Ash, C. J., Pseudovarieties, generalized varieties and similarly defined classes, to appear in J. Algebra.Google Scholar
3. Bonnet, R., On the cardinality of the set of initial intervals of a partially ordered set, Colloq. Math. Soc. Janos Bolyai 10 (1973), 189–198.Google Scholar
4. Burris, S. and Nelson, E., Embeddings Πm in the lattice equational classes of commutative semigroups, Proc. Amer. Math. Soc. 30 (1971), 37–39.Google Scholar
5. Eilenberg, S., Automata, languages and machines, Vol. B (Academic Press, 1976).Google Scholar
6. Eilenberg, S. and Schützenberger, M. P., On pseudovarieties, Advances in Mathematics 19 (1976), 413–418.Google Scholar
7. Higman, G., Ordering by divisibility in abstract algebras, Proc. London Math. Soc. 2 (1952), 326–336.Google Scholar
8. Korjakov, I. O., A sketch of the lattice of commutative nilpotent semigroups varieties, Semigroup Forum 24 (1982), 285–317.Google Scholar
9. Kruskal, J., The theory of well-quasi-ordering: a frequently discovered concept, J. Combinatorial Theory Ser. A 13 (1972), 297–305.Google Scholar
10. Laver, R., Better-quasi-orderings and a class of trees in Studies in foundations and combinatorics, Advances in Mathematics, Suppl. Studies 1 (1978), 31–48. Academic Press.Google Scholar
11. Nash-Williams, C. St. J. A., On well-quasi-ordering infinite trees, Proc. Camb. Phil. Soc. 61 (1965), 697–720.Google Scholar
12. Nelson, E., The lattice of equational classes of commutative semigroups, Can. J. Math. 23 (1971), 875–895.Google Scholar
13. Perkins, P., Bases for equational theories of semi-groups, J. Algebra 11 (1969), 298–314.Google Scholar
14. Rhodes, J., Infinite iteration of matrix semigroups, Part II: Structure theorem for arbitrary semigroups up to aperiodic morphism, PAM-121 (University of California, Berkeley, 1983).Google Scholar
15. Schwabauer, R., A note on commutative semigroups, Proc. Amer. Math. Soc. 20 (1969), 503–504.Google Scholar
16. Schwabauer, R., Commutative semigroup laws, Proc. Amer. Math. Soc. 22 (1969), 591–595.Google Scholar