Published online by Cambridge University Press: 20 November 2018
We define infinitely many sequences of integers 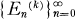 one sequence for each positive integer k ≦ 2 by
one sequence for each positive integer k ≦ 2 by
(1.1)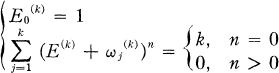
where 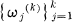 are the k-th roots of unity and (E(k))n is replaced by En(k) after multiplying out. An immediate consequence of (1.1) is
are the k-th roots of unity and (E(k))n is replaced by En(k) after multiplying out. An immediate consequence of (1.1) is
(1.2)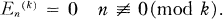
Therefore, we are interested in numbers of the form Esk(k) (s = 0, 1, 2, …; k = 2, 3, …).
Some special cases have been considered in the literature. For k = 2, we obtain the Euler numbers (see e.g. [8]). The case k = 3 is considered briefly by D. H. Lehmer [7], and the case k = 4 by Leeming [6] and Carlitz ([1]and [2]).