Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-15T09:22:30.154Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Results for the Generalized Lototsky Transform

Published online by Cambridge University Press:  20 November 2018

V. F. Cowling  and
C. L. Miracle
V. F. Cowling
Affiliation:
University of Kentucky
C. L. Miracle
Affiliation:
University of Minnesota
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A = (ank) and x = {sn} (n,k = 0,1,2, … ) be a matrix and a sequence of complex numbers, respectively. We write formally

(1.1)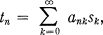

and say that the sequence x is summable A to the sum t or that the A matrix sums the sequence x to the value t if the series in (1.1) converges and

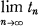
exists and equals t. We say that the matrix A is regular provided it sums every convergent sequence to its limit.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 418 - 435
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Agnew, R. P., Euler transformations, Amer. J. Math., 66 (1944), 318–338.Google Scholar
2. Agnew, R. P., The Lototsky method for evaluation of series, Mich. Math. J., 4 (1957), 105–128.Google Scholar
3. Jakimovski, A., A generalization of the Lototsky method, Mich. Math. J., 6 (1959), 277–290.Google Scholar
4. Karamata, J., Théorèmes sur la sommabilité exponentielle et d'autres sommabilités s'y rattachant, Mathematica, Cluj, 9 (1953), 164–178.Google Scholar
5. Lototsky, A. V., On a linear transformation of sequences and series, Ivanor. Gos. Ped. Inst. Uc. Zap. Fig.-Math. Nauki, 4 (1953), 61–91 (Russian).Google Scholar
6. Meir, A., On a theorem of A. Jakimovski on linear transformations, Mich. Math. J., 6 (1959), 359–361.Google Scholar
7. Okada, Y., Ueber die Annaherung analytischer Funktionen, Math. Zeit., 23 (1925), 62–71.Google Scholar
8. Vuckovic, V., The mutual inclusion of Karamata-Stirling methods of summation, Mich. Math. J., 6 (1959), 291–297.Google Scholar