Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Moy, Allen
and
Sally, Jr., Paul J.
1984.
Supercuspidal representations of SLn
over a p-adic field: the tame case.
Duke Mathematical Journal,
Vol. 51,
Issue. 1,
Shahidi, Freydoon
1991.
Harmonic Analysis on Reductive Groups.
Vol. 101,
Issue. ,
p.
277.
Henniart, Guy
and
Herb, Rebecca
1995.
Automorphic induction for GL(n)
(over local nonarchimedean fields).
Duke Mathematical Journal,
Vol. 78,
Issue. 1,
Goldberg, David
2006.
Reducibility for SUn and Generic Elliptic Representations.
Canadian Journal of Mathematics,
Vol. 58,
Issue. 2,
p.
344.
Chao, Kuok Fai
and
Li, Wen-Wei
2014.
DualR-groups of the inner forms of SL(N).
Pacific Journal of Mathematics,
Vol. 267,
Issue. 1,
p.
35.
Choiy, Kwangho
and
Goldberg, David
2015.
Transfer of R-groups between p-adic inner forms of SL n.
Manuscripta Mathematica,
Vol. 146,
Issue. 1-2,
p.
125.
Choiy, Kwangho
2016.
The Local Langlands Conjecture for thep-Adic Inner Form of Sp4.
International Mathematics Research Notices,
p.
rnw043.
Gao, Fan
2023.
R-GROUP AND WHITTAKER SPACE OF SOME GENUINE REPRESENTATIONS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 22,
Issue. 1,
p.
213.


 be the Weyl group of
be the Weyl group of 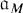 . It follows from a recent work of James Arthur
. It follows from a recent work of James Arthur 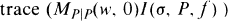
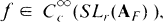
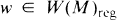
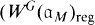 in the notation of [
in the notation of [