Article contents
Some Results on the Center of an Algebra of Operators on VN(G) for the Heisenberg group
Published online by Cambridge University Press: 20 November 2018
Extract
Let G be an amenable locally compact group. We will use the terminology of [3] and denote by VN(G) the Von Neumann algebra of the regular representation and by A(G) its predual, which is the algebra of the coefficients of the regular representation. The Von Neumann algebra VN(G) is, in a natural fashion, a module with respect to A(G) [3].
The algebra 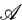 of bounded linear operators on VN(G), which commute
with the action of A(G), has been studied in [6] and in [1]. If UCB(Ĝ) is the space of the elements of VN(G) of the form vT, for some v in A(G) and some T in VN(G) (see for instance [4]), in [6] and in [1] it is proved that, for any amenable locally compact group there exists an isometric bijection between
of bounded linear operators on VN(G), which commute
with the action of A(G), has been studied in [6] and in [1]. If UCB(Ĝ) is the space of the elements of VN(G) of the form vT, for some v in A(G) and some T in VN(G) (see for instance [4]), in [6] and in [1] it is proved that, for any amenable locally compact group there exists an isometric bijection between 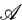 and UCB(Ĝ)*.
and UCB(Ĝ)*.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981
References
- 3
- Cited by


