Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ginsburg, John
1976.
On the Stone-Čech compactification of the space of closed sets.
Transactions of the American Mathematical Society,
Vol. 215,
Issue. 0,
p.
301.
Holá, L'ubica
and
Pelant, Jan
2002.
Recent Progress in General Topology II.
p.
253.
Cao, Jiling
Nogura, Tsugunori
and
Tomita, A.H.
2004.
Countable compactness of hyperspaces and Ginsburg's questions.
Topology and its Applications,
Vol. 144,
Issue. 1-3,
p.
133.
Hrušák, Michael
Hernández-Hernández, Fernando
and
Martínez-Ruiz, Iván
2007.
Pseudocompactness of hyperspaces.
Topology and its Applications,
Vol. 154,
Issue. 17,
p.
3048.
Juhász, István
and
Vaughan, Jerry E.
2007.
Countably compact hyperspaces and Frolík sums.
Topology and its Applications,
Vol. 154,
Issue. 12,
p.
2434.
Jardón, Daniel
2012.
Ultracompleteness of hyperspaces of compact sets.
Acta Mathematica Hungarica,
Vol. 137,
Issue. 1-2,
p.
139.
Kim, Junhui
2013.
A non-2-starcompact, pseudocompact Tychonoff space whose hyperspace is 2-starcompact.
Topology and its Applications,
Vol. 160,
Issue. 1,
p.
126.
Hrušák, Michael
2014.
Recent Progress in General Topology III.
p.
601.
Kemoto, N.
Ortiz-Castillo, Y.F.
and
Rojas-Hernández, R.
2014.
On C -embeddedness of hyperspaces.
Topology and its Applications,
Vol. 162,
Issue. ,
p.
34.
García-Ferreira, S.
and
Ortiz-Castillo, Y. F.
2018.
Pseudocompact Topological Spaces.
Vol. 55,
Issue. ,
p.
77.
Hernández-Hernández, F.
and
Hrušák, M.
2018.
Pseudocompact Topological Spaces.
Vol. 55,
Issue. ,
p.
253.
Ortiz-Castillo, Y.F.
Rodrigues, V.O.
and
Tomita, A.H.
2018.
Small cardinals and the pseudocompactness of hyperspaces of subspaces of βω.
Topology and its Applications,
Vol. 246,
Issue. ,
p.
9.
Tachtsis, Eleftherios
2019.
On ultracompact spaces in ZF.
Topology and its Applications,
Vol. 263,
Issue. ,
p.
257.
Guzmán, O.
Hrušák, M.
Rodrigues, V.O.
Todorčević, S.
and
Tomita, A.H.
2022.
Maximal almost disjoint families and pseudocompactness of hyperspaces.
Topology and its Applications,
Vol. 305,
Issue. ,
p.
107872.
Corral, Cesar
and
de O. Rodrigues, Vinicius
2024.
New examples of MAD families with pseudocompact hyperspaces.
Topology and its Applications,
Vol. 342,
Issue. ,
p.
108773.
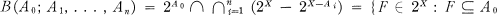 and
and 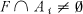 for all
for all 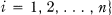 .
.

