Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T23:30:24.545Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Results on v-Multiplication Rings

Published online by Cambridge University Press:  20 November 2018

Malcolm Griffin
Malcolm Griffin*
Affiliation:
Applied Mathematics Division, D.S.I.R., Wellington, New Zealand
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

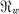A family Ω of valuations of the field K is said to be of finite character if only a finite number of valuations are non-zero at any non-zero element of K. If w ∈ Ω has ring and maximal ideal 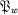, then A = ∩w∈Ω 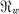is said to be defined by Ω and 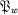∩ A is a prime ideal called the centre of w on A and denoted by Z(w). If 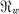= Az(w), then w is said to be an essential valuation for A. A domain defined by a family of finite character in which every valuation is essential is called a ring of Krull type.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 710 - 722
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Conrad, Paul, Some structure theorems for lattice ordered groups, Trans. Amer. Math. Soc., 99 (1961), 212–240.Google Scholar
2. Griffin, Malcolm, Families of finite character and essential valuations (to appear in Trans. Amer. Math. Soc).Google Scholar
3. Griffin, Malcolm, Rings of Krull type (to appear in J. Reine Angew. Math.).Google Scholar
4. Jaffard, Paul, Les systèmes d'idéaux (Paris, 1960).Google Scholar
5. Jensen, Chr. U., On characterisations of Prufer rings, Math. Scand., 13 (1963), 90–98.Google Scholar
6. Krull, Wolfgang, Idealtheorie, Ergebnisse der Math., vol. 4 (Berlin, 1935).Google Scholar
7. Ribenboim, Paulo, Sur les groupes totalement ordonnés et l'arithmétique des anneaux de valuation., Summa Brasil. Math., 4 (1958), 1–64.Google Scholar
8. Zariski, Oscar and Samuel, Pierre, Commutative algebra, Vol. I (Princeton, 1958).Google Scholar
9. Zariski, Oscar and Samuel, Pierre, Commutative algebra, Vol. II (Princeton, 1960).Google Scholar