Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T17:29:15.277Z Has data issue: false hasContentIssue false
  • English
  • Français

Spaces of knotted circles and exotic smooth structures

Part of: Differential topology PL-topology

Published online by Cambridge University Press:  24 August 2020

Gregory Arone  and
Markus Szymik
Gregory Arone
Affiliation:
Department of Mathematics, Stockholm University, Stockholm, Sweden e-mail: gregory.arone@math.su.se
Markus Szymik*
Affiliation:
Department of Mathematical Sciences, NTNU Norwegian University of Science and Technology, Trondheim, Norway
*
e-mail: markus.szymik@ntnu.no
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

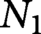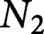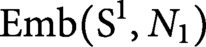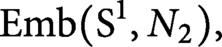Suppose that $N_1$ and $N_2$ are closed smooth manifolds of dimension n that are homeomorphic. We prove that the spaces of smooth knots, $ \operatorname {\mathrm {Emb}}(\mathrm {S}^1, N_1)$ and $ \operatorname {\mathrm {Emb}}(\mathrm {S}^1, N_2),$ have the same homotopy 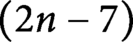$(2n-7)$ -type. In the four-dimensional case, this means that the spaces of smooth knots in homeomorphic 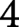$4$ -manifolds have sets 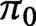$\pi _0$ of components that are in bijection, and the corresponding path components have the same fundamental groups 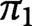$\pi _1$ . 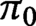The result about $\pi _0$ is well-known and elementary, but the result about 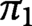$\pi _1$ appears to be new. The result gives a negative partial answer to a question of Oleg Viro. Our proof uses the Goodwillie–Weiss embedding tower. We give a new model for the quadratic stage of the Goodwillie–Weiss tower, and prove that the homotopy type of the quadratic approximation of the space of knots in N does not depend on the smooth structure on N. Our results also give a lower bound on 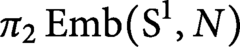$\pi _2 \operatorname {\mathrm {Emb}}(\mathrm {S}^1, N)$ . We use our model to show that for every choice of basepoint, each of the homotopy groups, 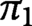$\pi _1$ and 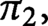$\pi _2,$ of 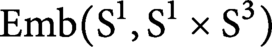$ \operatorname {\mathrm {Emb}}(\mathrm {S}^1, \mathrm {S}^1\times \mathrm {S}^3)$ contains an infinitely generated free abelian group.

Keywords

Knotsembeddingsexotic smooth structuresfunctor calculus

MSC classification

Primary: 57Q45: Knots and links (in high dimensions) 57R55: Differentiable structures
Secondary: 57R40: Embeddings 57R42: Immersions
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 1 , February 2022 , pp. 1 - 23
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2020

Footnotes

The authors thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the program “Homotopy harnessing higher structures” where work on this paper was undertaken. This work was supported by EPSRC grant no EP/K032208/1. G. A. was supported by the Swedish Research Council, grant number 2016-05440.

References

Arone, G. and Kankaanrinta, M., On the functoriality of the blow-up construction. Bull. Belg. Math. Soc. Simon Stevin 17(2010), 821–832.CrossRefGoogle Scholar
Budney, R., A family of embedding spaces. groups, homotopy and configuration spaces. Geometry Topology Monograph, 13, Geometry Topology Publications, Coventry, England, 2008, pp. 41–83.CrossRefGoogle Scholar
Budney, R. and Gabai, D., Knotted  $3$ -balls in ${S}^4$ . Preprint, 2019. arXiv:1912.09029 Google Scholar
Dax, J.-P., Étude homotopique des espaces de plongements. Ann. Sci. École Norm. Sup. 5(1972), 303–377.CrossRefGoogle Scholar
Dold, A. and Whitney, H., Classification of oriented sphere bundles over a 4-complex. Ann. Math. 69(1959), 667–677.CrossRefGoogle Scholar
Goodwillie, T. G. and Klein, J. R., Multiple disjunction for spaces of smooth embeddings. J. Topol. 8(2015), 651–674.CrossRefGoogle Scholar
Goodwillie, T. G., Klein, J. R., and Weiss, M. S., Spaces of smooth embeddings, disjunction and surgery . In: Surveys on surgery theory. Vol. 2, Annals of Mathematics Studies, 149, Princeton University Press, Princeton, NJ, 2001, pp. 221–284.Google Scholar
Goodwillie, T. G., Klein, J. R., and Weiss, M. S., A Haefliger style description of the embedding calculus tower. Topology 42(2003), 509–524.CrossRefGoogle Scholar
Hirzebruch, F. and Hopf, H., Felder von Flächenelementen in 4-dimensionalen Mannigfaltigkeiten. Math. Ann. 136(1958), 156–172.CrossRefGoogle Scholar
Lashof, R., Embedding spaces. Ill. J. Math. 20(1976), 144–154.Google Scholar
Mather, M., Pull-backs in homotopy theory. Can. J. Math. 28(1976), 225–263.CrossRefGoogle Scholar
Milnor, J., Topological manifolds and smooth manifolds . 1963 Proceedings of ICM, Institute Mittag-Leffler, Djursholm, Stockholm, 1962, pp. 132–138.Google Scholar
Moriya, S., Models for knot spaces and Atiyah duality. Preprint, 2020. arXiv:2003.03815 Google Scholar
Nash, J., A path space and the Stiefel–Whitney classes. Proc. Natl. Acad. Sci 41(1955), 320–321.CrossRefGoogle ScholarPubMed
Thom, R., Espaces fibrés en sphères et carrés de Steenrod. Ann. Sci. Ecole Norm. Sup. 69(1952), 109–182.CrossRefGoogle Scholar
Viro, O., Space of smooth 1-knots in a 4-manifold: is its algebraic topology sensitive to smooth structures? Arnold Math. J. 1(2015), 83–89.CrossRefGoogle Scholar
Weiss, M., Calculus of embeddings. Bull. Am. Math. Soc. 33(1996), 177–187.CrossRefGoogle Scholar
Weiss, M., Embeddings from the point of view of immersion theory I. Geom. Topol. 3(1999), 67–101.CrossRefGoogle Scholar