Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T21:08:24.735Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral Estimates for Towers of Noncompact Quotients

Published online by Cambridge University Press:  20 November 2018

Anton Deitmar  and
Werner Hoffman
Anton Deitmar
Affiliation:
Mathematisches Institut, Im Neuenheimer Feld 288, 69126 Heidelberg, Germany email: anton@mathi.uni-heidelberg.de
Werner Hoffman
Affiliation:
Humboldt-Universität zu Berlin, Institut für Mathematik, Jägerstr. 10/11, 10117 Berlin, Germany email: hoffmann@mathematik.hu-berlin.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

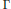We prove a uniform upper estimate on the number of cuspidal eigenvalues of the $\Gamma$-automorphic Laplacian below a given bound when 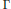$\Gamma$ varies in a family of congruence subgroups of a given reductive linear algebraic group. Each 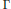$\Gamma$ in the family is assumed to contain a principal congruence subgroup whose index in 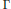$\Gamma$ does not exceed a fixed number. The bound we prove depends linearly on the covolume of 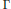$\Gamma$ and is deduced from the analogous result about the cut-off Laplacian. The proof generalizes the heat-kernel method which has been applied by Donnelly in the case of a fixed lattice 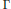$\Gamma$.

Keywords

11F7258G2522E40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 2 , 01 April 1999 , pp. 266 - 293
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Arthur, J., A trace formula for reductive groups I: Terms associated to classes in G(Q). DukeMath. J. 45 (1978), 911–952.Google Scholar
[2] Arthur, J., A trace formula for reductive groups II: Applications of a truncation operator. Comp.Math. 40 (1980), 87–121.Google Scholar
[3] Borel, A., Some finiteness properties of adele groups over number fields. Inst. Hautes Études Sci. Publ. Math. 16 (1963), 5–30.Google Scholar
[4] Chernoff, P., Essential self-adjointness of powers of generators of hyperbolic equations. J. Funct.Anal. 12 (1973), 401–414.Google Scholar
[5] Donnelly, H., Asymptotic expansions for the compact quotients of properly discontinuous group actions. Illinois J. Math. 23 (1979), 485–496.Google Scholar
[6] Donnelly, H., On the cuspidal spectrum for finite volume symmetric spaces. J. Differential Geom. 17 (1982), 239–253.Google Scholar
[7] Friedman, A., Partial differential equations of parabolic type. Prentice-Hall, Englewood Cliffs, 1964.Google Scholar
[8] Ji, L., The trace class conjecture for arithmetic groups. J. Differential Geom. 48 (1998), 165–203.Google Scholar
[9] Mostow, G. D., Self-adjoint groups. Ann. ofMath. 62 (1955), 44–55.Google Scholar
[10] Müller, W., The trace class conjecture in the theory of automorphic forms. Ann.Math. 130 (1989), 473–529.Google Scholar
[11] Müller, W., The trace class conjecture in the theory of automorphic forms. II. Geom. Funct. Anal. 8 (1998), 315–355.Google Scholar
[12] Osborne, M. S. and G.Warner, The Selberg trace formula II: Partition, reduction, truncation. Pacific J. Math. 106 (1983), 307–496.Google Scholar
[13] Ray, D. B. and Singer, I. M., R-torsion and the Laplacian on Riemannian manifolds. Advances in Math. 7 (1971), 145–210.Google Scholar