Article contents
Stability and Categoricity of Lattices
Published online by Cambridge University Press: 20 November 2018
Extract
This paper is a contribution to applied stability theory. Our purpose is to investigate the complexity of lattices by determining the stability of their first order theories.
Stability measures the complexity of a theory T by counting the number of different “kinds” of elements in models of T. The notion of ω-stability was introduced by Morley [26] in 1965 and generalized by Shelah [31] in 1969. Shelah classified all first order theories according to their stability properties.
Stability and 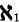 -categoricity are closely related (see [26] and [1]). In fact, the notions of stable, superstable and ω-stable can be regarded as successive approximations of
-categoricity are closely related (see [26] and [1]). In fact, the notions of stable, superstable and ω-stable can be regarded as successive approximations of 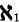 -categorical.
-categorical. 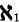 -categoricity is a very strong property while stability, superstability and ω-stability facilitate the classification of more “complex” theories.
-categoricity is a very strong property while stability, superstability and ω-stability facilitate the classification of more “complex” theories.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981
References
- 7
- Cited by


