Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-22T23:27:55.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of rotation relations in 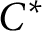$C^*$-algebras

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  21 May 2020

Jiajie Hua  and
Qingyun Wang
Jiajie Hua*
Affiliation:
College of Mathematics, Physics and Information Engineering, Jiaxing University, Jiaxing, Zhejiang314000, China
Qingyun Wang
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR97403, USA e-mail: qingyunw@uoregon.edu
*
e-mail: huajiajie2006@hotmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 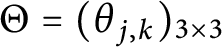$\Theta =(\theta _{j,k})_{3\times 3}$ be a nondegenerate real skew-symmetric $3\times 3$ matrix, where 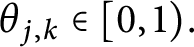$\theta _{j,k}\in [0,1).$ For any 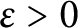$\varepsilon>0$ , we prove that there exists 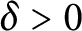$\delta>0$ satisfying the following: if 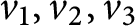$v_1,v_2,v_3$ are three unitaries in any unital simple separable 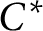$C^*$ -algebra A with tracial rank at most one, such that

$$\begin{align*}\|v_kv_j-e^{2\pi i \theta_{j,k}}v_jv_k\|<\delta \,\,\,\, \mbox{and}\,\,\,\, \frac{1}{2\pi i}\tau(\log_{\theta}(v_kv_jv_k^*v_j^*))=\theta_{j,k}\end{align*}$$
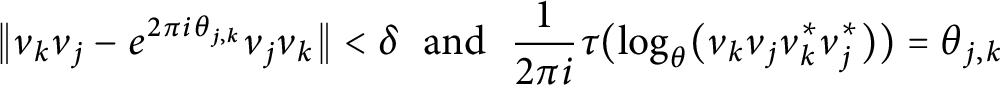
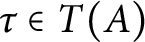for all $\tau \in T(A)$ and 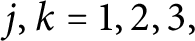$j,k=1,2,3,$ where $\log _{\theta }$ is a continuous branch of logarithm (see Definition 4.13) for some real number 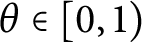$\theta \in [0, 1)$ , then there exists a triple of unitaries 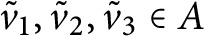$\tilde {v}_1,\tilde {v}_2,\tilde {v}_3\in A$ such that
$$\begin{align*}\tilde{v}_k\tilde{v}_j=e^{2\pi i\theta_{j,k} }\tilde{v}_j\tilde{v}_k\,\,\,\,\mbox{and}\,\,\,\,\|\tilde{v}_j-v_j\|<\varepsilon,\,\,j,k=1,2,3.\end{align*}$$

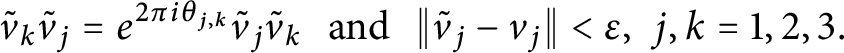
The same conclusion holds if $\Theta $ is rational or nondegenerate and A is a nuclear purely infinite simple 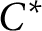$C^*$ -algebra (where the trace condition is vacuous).

If $\Theta $ is degenerate and A has tracial rank at most one or is nuclear purely infinite simple, we provide some additional injectivity conditions to get the above conclusion.

Keywords

rotation relationsC*-algebrasstabilitynoncommutative toriunitary

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L35: Classifications of $C^*$-algebras
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 4 , August 2021 , pp. 1171 - 1203
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berg, I. D. and Davidson, K. R., Almost commuting matrices and the Brown-Douglas-Fillmore theorem . Bull. Amer. Math. Soc. 16(1987), no. 1, 97–100.CrossRefGoogle Scholar
Chakraborty, S., Some remarks on ${K}_0$ of noncommutative tori. Math. Scand. 126(2020), no. 2, 387–400.CrossRefGoogle Scholar
Dadarlat, M., Morphisms of simple tracially AF algebras . Int. J. Math. 15(2004), no. 9, 919–957.CrossRefGoogle Scholar
Dadarlat, M. and Loring, T. A., A universal multicoefficient theorem for the Kasparov groups . Duke Math. J. 84(1996), no. 2, 355–377.CrossRefGoogle Scholar
Davidson, K. R., Almost commuting Hermitian matrices . Math. Scand. 56(1985), no. 2, 222–240.CrossRefGoogle Scholar
Eilers, S. and Loring, T. A., Computing contingencies for stable relations . Int. J. Math. 10(1999), no. 3, 301–326.CrossRefGoogle Scholar
Eilers, S., Loring, T. A., and Pedersen, G. K., Stability of anticommutation relations: an application of noncommutative CW complexes . J. Reine Angew. Math. 499(1998), 101–143.Google Scholar
Eilers, S., Loring, T. A., and Pedersen, G. K., Morphisms of extensions of ${C}^{\ast }$ -algebras: pushing forward the Busby invariant . Adv. Math. 147(1999), no. 1, 74–109.CrossRefGoogle Scholar
Elliott, G. A., On the K-theory of the C*-algebra generated by a projective representation of a torsion free discrete abelian group . In: Operator algebras and group representations, I, Pitman, Boston, MA, 1984, pp. 157–184.Google Scholar
Elliott, G. A. and Li, H., Strong Morita equivalence of higher-dimensional noncommutative tori. II . Math. Ann. 341(2008), 825–844.CrossRefGoogle Scholar
Exel, R., The soft torus and applications to almost commuting matrices . Pacific J. Math. 160(1993), no. 2, 207–217.CrossRefGoogle Scholar
Exel, R. and Loring, T. A., Almost commuting unitary matrices . Proc. Amer. Math. Soc. 106(1989), no. 4, 913–915.CrossRefGoogle Scholar
Exel, R. and Loring, T. A., Invariants of almost commuting unitaries . J. Funct. Anal. 95(1991), no. 2, 364–376.CrossRefGoogle Scholar
Farsi, C., Soft non-commutative toral ${C}^{\ast }$ -algebras. J. Funct. Anal. 151(1997), no. 1, 35–49.CrossRefGoogle Scholar
Halmos, P. R., Some unsolved problems of unknown depth about operators on Hilbert space . Proc. Roy. Soc. Edinburgh Sect. A. 76(1976/77), no. 1, 67–76.CrossRefGoogle Scholar
Hua, J. and Lin, H., Rotation algebras and the Exel trace formula . Canad. J. Math. 67(2015), no. 2, 404–423.CrossRefGoogle Scholar
Hunton, J. and Shchukin, M., The $K$ -theory of ${C}^{\ast }$ -algebras with finite dimensional irreducible representations. Integral Equat. Operat. Theory 54(2006), no. 1, 89–96.CrossRefGoogle Scholar
Itzá-Ortiz, B. A. and Phillips, N. C., Realization of a simple higher-dimensional noncommutative torus as a transformation group ${C}^{\ast}$ -algebra. Bull. Lond. Math. Soc. 40(2008), no. 2, 217–226.CrossRefGoogle Scholar
Li, H., Strong Morita equivalence of higher-dimensional noncommutative tori . J. Reine Angew. Math. 576(2004), 167–180.Google Scholar
Lin, H., Almost commuting selfadjoint matrices and applications . In: Operator algebras and their applications (Waterloo, ON, 1994/1995), Fields Inst. Commun., 13, Amer. Math. Soc., Providence, RI, 1997, pp. 193–233.Google Scholar
Lin, H., Almost multiplicative morphisms and some applications . J. Operat. Theory 37(1997), no. 1, 121–154.Google Scholar
Lin, H., An introduction to the classification of amenable ${C}^{\ast }$ -algebras. World Scientific Publishing Co., Inc., River Edge, NJ, 2001.CrossRefGoogle Scholar
Lin, H., The tracial topological rank of ${C}^{\ast }$ -algebra. Proc. Lond. Math. Soc. 83(2001), no. 1, 199–234.CrossRefGoogle Scholar
Lin, H., A separable Brown-Douglas-Fillmore theorem and weak stability . Trans. Am. Math. Soc. 356(2004), no. 7, 2889–2925.CrossRefGoogle Scholar
Lin, H., Classification of homomorphisms and dynamical systems . Trans. Am. Math. Soc. 359(2007), no. 2, 859–895.CrossRefGoogle Scholar
Lin, H., Homotopy of unitaries in simple ${C}^{\ast }$ -algebras with tracial rank one. J. Funct. Anal. 258(2010), 1822–1882.CrossRefGoogle Scholar
Lin, H., Homomorphisms from AH-algebras . J. Topol. Anal. 9(2017), no. 1, 67–125.CrossRefGoogle Scholar
Loring, T. A., $K$ -theory and asymptotically commuting matrices. Canad. J. Math. 40(1988), no. 1, 197–216.CrossRefGoogle Scholar
Phillips, N. C., Every simple higher dimensional noncommutative torus is an ${AT}$ algebra. Preprint, 2006. arXiv:math.OA/0609783.Google Scholar
Pimsner, M. and Voiculescu, D., Exact sequences for $K$ -groups and Ext-groups of certain crossed product ${C}^{\ast }$ -algebras . J. Operat. Theory 4(1980), no. 1, 93–118.Google Scholar
Rieffel, M. A., C*-algebras associated with irrational rotations . Pacific J. Math. 93(1981), no. 2, 415–429.CrossRefGoogle Scholar
Rieffel, M. A., Non-commutative tori–a case study of non-commutative differentiable manifolds . In: Kaminker, J. (ed.), Geometric and topological invariants of elliptic operators, Contemporary Mathematics, 105, Brunswick, ME, 1988, pp. 191–211.Google Scholar
Rosenberg, J. and Schochet, C., The Kunneth theorem and the universal coefficient theorem for Kasparov’s generalized K-functor . Duke Math. J. 55(1987), 431–474.CrossRefGoogle Scholar
Rosenthal, P., Research problems: Are almost commuting matrices near commuting matrices? Amer. Math. 76(1969), no. 8, 925–926.CrossRefGoogle Scholar
Schochet, C., Topological methods for ${C}^{\ast }$ -algebras. IV. Mod $p$  homology . Pacific J. Math. 114(1984), no. 2, 447–468.CrossRefGoogle Scholar
Thomsen, K., Traces, unitary characters and crossed products by ${\textrm{Z}}$ . Publ. Res. Inst. Math. Sci. 31(1995), no. 6, 1011–1029.CrossRefGoogle Scholar
Voiculescu, D., Remarks on the singular extension in the ${C}^{\ast }$ -algebra of the Heisenberg group. J. Operat. Theory 5(1981), 147–170.Google Scholar
Voiculescu, D., Asymptotically commuting finite rank unitary operators without commuting approximants. Acta Sci. Math. (Szeged) 45(1983), no. 1, 429–431.Google Scholar