Published online by Cambridge University Press: 20 November 2018
We consider, in this work, the asymptotic behaviour for large λ, of a Fourier integral
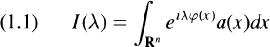
where 𝜑(x) is in general a C∞ function and a(x) a C∞ function with compact support. It is well known that the asymptotic behaviour of this integral is controlled by the behaviour of 𝜑 at its critical points (i.e., points where 𝜕𝜑/𝜕xj(x) = 0) and is given by local contributions at these points ([1], [3], [7], [9]).
In general, one assumes the hypothesis of non degenerate isolated critical point, namely that the determinant of the second derivative at the critical point is non zero.