Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T16:07:30.680Z Has data issue: false hasContentIssue false
  • English
  • Français

The Steklov Problem on Differential Forms

Part of: Spectral theory and eigenvalue problems Partial differential equations on manifolds; differential operators

Published online by Cambridge University Press:  07 January 2019

Mikhail A. Karpukhin
Mikhail A. Karpukhin*
Affiliation:
Department of Statistics and Mathematics, McGill University, Montreal QC H4A3J3, Canada Email: mikhail.karpukhin@mail.mcgill.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study spectral properties of the Dirichlet-to-Neumann map on differential forms obtained by a slight modification of the definition due to Belishev and Sharafutdinov. The resulting operator 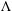$\unicode[STIX]{x039B}$ is shown to be self-adjoint on the subspace of coclosed forms and to have purely discrete spectrum there. We investigate properties of eigenvalues of 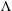$\unicode[STIX]{x039B}$ and prove a Hersch–Payne–Schiffer type inequality relating products of those eigenvalues to eigenvalues of the Hodge Laplacian on the boundary. Moreover, non-trivial eigenvalues of 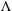$\unicode[STIX]{x039B}$ are always at least as large as eigenvalues of the Dirichlet-to-Neumann map defined by Raulot and Savo. Finally, we remark that a particular case of 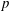$p$-forms on the boundary of a 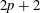$2p+2$-dimensional manifold shares many important properties with the classical Steklov eigenvalue problem on surfaces.

Keywords

Dirichlet-to-Neumann mapdifferential formSteklov eigenvalueshape optimization

MSC classification

Primary: 58J50: Spectral problems; spectral geometry; scattering theory
Secondary: 58J32: Boundary value problems on manifolds 35P15: Estimation of eigenvalues, upper and lower bounds
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 2 , April 2019 , pp. 417 - 435
Copyright
© Canadian Mathematical Society 2018 

References

Belishev, M. and Sharafutdinov, V., Dirichlet to Neumann operator on differential forms . Bull. Sci. Math. 132(2008), no. 2, 128–145. https://doi.org/10.1016/j.bulsci.2006.11.003.Google Scholar
Fraser, A. and Schoen, R., The first Steklov eigenvalue, conformal geometry, and minimal surfaces . Adv. Math. 226(2011), no. 5, 4011–4030. https://doi.org/10.1016/j.aim.2010.11.007.Google Scholar
Fraser, A. and Schoen, R., Sharp eigenvalue bounds and minimal surfaces in the ball . Invent. Math. 203(2016), no. 3, 823–890. https://doi.org/10.1007/s00222-015-0604-x.Google Scholar
Girouard, A. and Polterovich, I., Shape optimization for low Neumann and Steklov eigenvalues . Math. Methods Appl. Sci. 33(2010), no. 4, 501–516. https://doi.org/10.1002/mma.1222.Google Scholar
Girouard, A. and Polterovich, I., Upper bounds for Steklov eigenvalues on surfaces . Electron. Res. Announc. Math. Sci. 19(2012), 77–85. https://doi.org/10.3934/era.2012.19.77.Google Scholar
Girouard, A. and Polterovich, I., Spectral geometry of the Steklov problem . J. Spectr. Theory 7(2017), no. 2, 321–359. https://doi.org/10.4171/JST/164.Google Scholar
Hersch, J., Payne, L. E., and Schiffer, M. M., Some inequalities for Stekloff eigenvalues . Arch. Rational Mech. Anal. 57(1975), 99–114. https://doi.org/10.1007/BF00248412.Google Scholar
Ikeda, A. and Taniguchi, Y., Spectra and eigenforms of the Laplacian on $\mathbb{S}^{n}$ and $P^{n}(\mathbb{C})$ . Osaka J. Math. 15 (1978), no. 3, 515–546.Google Scholar
Joshi, M. S. and Lionheart, W. R. B., An inverse boundary value problem for harmonic differential forms . Asymptot. Anal. 41(2005), no. 2, 93–106.Google Scholar
Karpukhin, M., Bounds between Laplace and Steklov eigenvalues on nonnegatively curved manifolds . Electron. Res. Announc. Math. Sci. 24(2017), 100–109. https://doi.org/10.3934/era.2017.24.011.Google Scholar
Krupchyk, K., Kurylev, Y., and Lassas, M., Reconstruction of Betti numbers of manifolds for anisotropic Maxwell and Dirac systems . Comm. Anal. Geom. 18(2010), no. 5, 963–985. https://doi.org/10.4310/CAG.2010.v18.n5.a4.Google Scholar
Kwong, K.-K., Some sharp Hodge Laplacian and Steklov eigenvalue estimates for differential forms . Calc. Var. Partial Differential Equations 55(2016), no. 2, Art. 38, 14 pp. https://doi.org/10.1007/s00526-016-0977-8.Google Scholar
Raulot, S. and Savo, A., On the first eigenvalue of the Dirichlet-to-Neumann operator on forms . J. Funct. Anal. 262(2012), no. 3, 889–914. https://doi.org/10.1016/j.jfa.2011.10.008.Google Scholar
Raulot, S. and Savo, A., On the spectrum of the Dirichlet-to-Neumann operator acting on forms of a Euclidean domain . J. Geom. Phys. 77(2014), 1–12. https://doi.org/10.1016/j.geomphys.2013.11.002.Google Scholar
Schwarz, G., Hodge decomposition — a method for solving boundary value problems. Lecture Notes in Mathematics, 1607. Springer-Verlag, Berlin, 1995.Google Scholar
Sharafutdinov, V. and Shonkwiler, C., The complete Dirichlet-to-Neumann map for differential forms . J. Geom. Anal. 23(2013), no. 4, 2063–2080. https://doi.org/10.1007/s12220-012-9320-6.Google Scholar
Shi, Y. and Yu, C., Trace and inverse trace of Steklov eigenvalues . J. Differential Equations 261(2016), no. 3, 2026–2040. https://doi.org/10.1016/j.jde.2016.04.023.Google Scholar
Shi, Y. and Yu, C., Trace and inverse trace of Steklov eigenvalues II . J. Differential Equations 262(2017), no. 3, 2592–2607. https://doi.org/10.1016/j.jde.2016.11.018.Google Scholar
Shonkwiler, C., Poincaré duality angles and the Dirichlet-to-Neumann operator . Inverse Problems 29(2013), no. 4. https://doi.org/10.1088/0266-5611/29/4/045007.Google Scholar
Thirring, W., A course in mathematical physics. 2. Second edition. Translated from German by Evans M. Harrell. Springer-Verlag, New York, 1986. https://doi.org/10.1007/978-1-4419-8762-4.Google Scholar
Yang, L. and Yu, C., A higher dimensional generalization of Hersch–Payne–Schiffer inequality for Steklov eigenvalues . J. Funct. Anal. 272(2017), no. 10, 4122–4130. https://doi.org/10.1016/j.jfa.2017.02.023.Google Scholar
Yang, L. and Yu, C., Estimates for higher Steklov eigenvalues . J. Math. Phys. 58(2017), no. 2. https://doi.org/10.1063/1.4976806.Google Scholar