Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T21:46:19.440Z Has data issue: false hasContentIssue false
  • English
  • Français

Strictly Singular and Cosingular Multiplications

Published online by Cambridge University Press:  20 November 2018

Mikael Lindström ,
Eero Saksman  and
Hans-Olav Tylli
Mikael Lindström
Affiliation:
Department of Mathematics, Åbo Akademi University, Fänriksgatan 3 B, FIN-20500 Åbo, Finland, email: mlindstr@abo.fi
Eero Saksman
Affiliation:
Department of Mathematics and Statistics, P.O. Box 35 (MaD), FIN-40014 University of Jyväskylä, Finland, email: saksman@maths.jyu.fi
Hans-Olav Tylli
Affiliation:
Department of Mathematics and Statistics, P.O. Box 68, Gustaf Hällströmin katu 2b, FIN-00014 University of Helsinki, Finland, email: hojtylli@cc.helsinki.fi
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 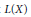$L(X)$ be the space of bounded linear operators on the Banach space 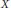$X$. We study the strict singularity and cosingularity of the two-sided multiplication operators 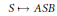$S\,\mapsto \,ASB$ on 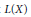$L(X)$, where 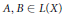$A,\,B\,\in \,L(X)$ are fixed bounded operators and 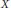$X$ is a classical Banach space. Let 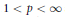$1\,<\,p\,<\,\infty $ and 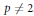$p\,\ne \,2$. Our main result establishes that the multiplication 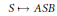$S\,\mapsto \,ASB$ is strictly singular on 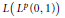$L\left( {{L}^{p}}\left( 0,\,1 \right) \right)$ if and only if the non-zero operators 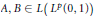$A,\,B\,\in \,L\left( {{L}^{p}}\left( 0,\,1 \right) \right)$ are strictly singular. 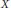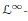We also discuss the case where $X$ is a ${\mathcal{L}^{1}}-$ or a ${{\mathcal{L}}^{\infty }}-$space, as well as several other relevant examples.

Keywords

47B4746B28
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 6 , 01 December 2005 , pp. 1249 - 1278
Copyright
Copyright © Canadian Mathematical Society 2005

References

[B1] Bourgain, J., New Classes of Lp-Spaces. Lecture Notes in Math. 889, Springer-Verlag, Berlin, 1981.Google Scholar
[B2] Bourgain, J., On the Dunford–Pettis property. Proc. Amer.Math. Soc. 81(1981), 265–272.Google Scholar
[BP] Bourgain, J. and Pisier, G., A construction of L∞-spaces and related Banach spaces. Bol. Soc. Brasil. Mat. 14(1983), 109–123.Google Scholar
[Ci] Cilia, R., A remark on the Dunford–Pettis property in L1(μ, X). Proc. Amer.Math. Soc. 120(1994), 183–184.Google Scholar
[C] Curto, R., Spectral theory of elementary operators. In: Elementary Operators and Applications, World Scientific, River Edge, NJ, 1991, pp. 3–52.Google Scholar
[DF] Defant, A. and Floret, K., Tensor norms and operator ideals. North-Holland, 1993.Google Scholar
[D] Diestel, J., A survey of results related to the Dunford–Pettis property. ContemporaryMath. 2 (1980), 15–60.Google Scholar
[DiF] Diestel, J. and Faires, B., Remarks on classical Banach operator ideals. Proc. Amer.Math. Soc. 58(1976), 189–196.Google Scholar
[E] Emmanuele, G., Remarks on weak compactness of operators on certain injective tensor products. Proc. Amer.Math. Soc. 116(1992), 473–476.Google Scholar
[FS] Feder, M. and Saphar, P., Spaces of compact operators and their dual spaces. Israel J. Math. 21(1975), 38–49.Google Scholar
[F] Fialkow, L. A., Structural properties of elementary operators. In: Elementary Operators and Applications, World Scientific, River Edge, NJ, 1991, pp. 55–113.Google Scholar
[KP] Kadec, M. I. and Pełczy ński, A., Bases, lacunary sequences and complemented subspaces in the spaces Lp. Studia Math. 21(1962), 161–176.Google Scholar
[K] Kalton, N. J., Spaces of compact operators. Math. Ann. 208(1973), 267–278.Google Scholar
[LT1] Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces. Lecture Notes in Math. 338, Springer-Verlag, 1973.Google Scholar
[LT2] Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces I. Sequence spaces. Springer-Verlag, 1977.Google Scholar
[LT3] Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces II. Function spaces. Springer-Verlag, 1979.Google Scholar
[LS] Lindström, M. and Schlüchtermann, G., Composition of operator ideals. Math. Scand. 84(1999), 284–296.Google Scholar
[M1] Mathieu, M., The norm problem for elementary operators. In: Recent Progress in Functional Analysis, North-Holland Math. Studies 189, Elsevier, Amsterdam, 2001, pp. 363–368.Google Scholar
[M2] Mathieu, M., Elementary operators on Calkin algebras. Irish Math. Soc. Bull. 46(2001), 33–42.Google Scholar
[Mi1] Milman, V. D., Some properties of strictly singular operators. Funct. Anal. Appl. 3(1969), 77–78.Google Scholar
[Mi2] Milman, V. D., Operators of class C0 and C* 0. Teor. Funktsiĭ Funktsional. Anal. i Prilozhen. 10(1970), 15–26.Google Scholar
[P] Pełczy ński, A., On strictly singular and strictly cosingular operators. I. Strictly singular and strictly cosingular operators in C(S)-spaces. II. Strictly singular and strictly cosingular operators in L(μ)-spaces. Bull. Acad. Polon. Sci. 13(1965), 31–41.Google Scholar
[Pi] Pietsch, A., Operator ideals. North-Holland, 1980.Google Scholar
[R] Racher, G., On the tensor product of weakly compact operators. Math. Ann. 294(1992), 267–275.Google Scholar
[Ro] Rosenthal, H. P., On quasi-complemented subspaces of Banach spaces, with an appendix on compactness of operators from Lp(μ) to Lr(ν). Funct, J.. Anal. 2(1969), 176–214.Google Scholar
[ST1] Saksman, E. and Tylli, H.-O., Weak compactness of multiplication operators on spaces of bounded linear operators. Math. Scand. 70(1992), 91–111.Google Scholar
[ST2] Saksman, E. and Tylli, H.-O., Rigidity of commutators and elementary operators on Calkin algebras. Israel J. Math. 108(1998), 217–236.Google Scholar
[ST3] Saksman, E. and Tylli, H.-O., The Apostol–Fialkow formula for elementary operators on Banach spaces. J. Funct. Anal. 161(1999), 1–26.Google Scholar
[V] Vala, K., On compact sets of compact operators. Ann. Acad. Sci. Fenn. Ser. A I Math. 351(1964).Google Scholar
[W] L.Weis, On perturbations of Fredholm operators in Lp(ν)-spaces. Proc. Amer. Math. Soc. 67(1977), 287–292.Google Scholar
[Wo] P.Wojtaszczyk, Banach spaces for analysts. Cambridge University Press, 1981.Google Scholar