Article contents
Strong Convergence of Pramarts in Banach Spaces
Published online by Cambridge University Press: 20 November 2018
Extract
Let E be a Banach space and 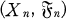 be an adapted sequence on the probability space
be an adapted sequence on the probability space 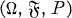 We denote by T the set of all bounded stopping times with respect to
We denote by T the set of all bounded stopping times with respect to 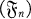 .
. 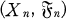 is called a pramart if
is called a pramart if
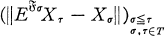
converges to zero in probability, uniformly in τ ≧ σ. The notion of pramart was introduced in [6]. A good property is the optional sampling property (see Theorem 2.4 in [6]). Furthermore the class of pramarts intersects the class of amarts, and every amart is a pramart if and only if dim E < ∞ ([2], see also [4]). Pramarts behave indeed quite differently than amarts. Although the class of pramarts is large, they have good convergence properties as is seen in the next two results of Millet-Sucheston, [6], [7].
THEOREM 1.1. Let 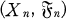 be a real-valued pramart of class (d), i.e.,
be a real-valued pramart of class (d), i.e.,
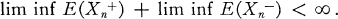
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981
References
- 8
- Cited by

